Vacuum Field Fluctuations

$$G^{(1)}(\tau, \delta\vec{r}) = <E^{*}(t, \vec{r})E(t+\tau, \vec{r}+\delta\vec{r})>$$

Its measurement is usually performed in an interferometer, employing absorption based detectors, which are not compatible with the detection of vacuum fields. We performed the first direct electric field correlation measurement on the electromagnetic vacuum state at terahertz (THz) frequencies at two space time points [1].

Our measurement scheme is based on electro-optic sampling (EOS) [2], a technique in which an ultrashort near-infrared probe pulse enables the measurement of the instantaneous free-running THz electric field by probing locally the birefringence induced in a detection crystal with second-order nonlinear susceptibility \(\chi^{(2)}\). EOS combined with 2 ultrashort femtosecond pulses, mutually delayed by a time tau, and fast detectors (see Fig.1) has already been employed to perform first and second order correlation of classical fields ([3,4]).  

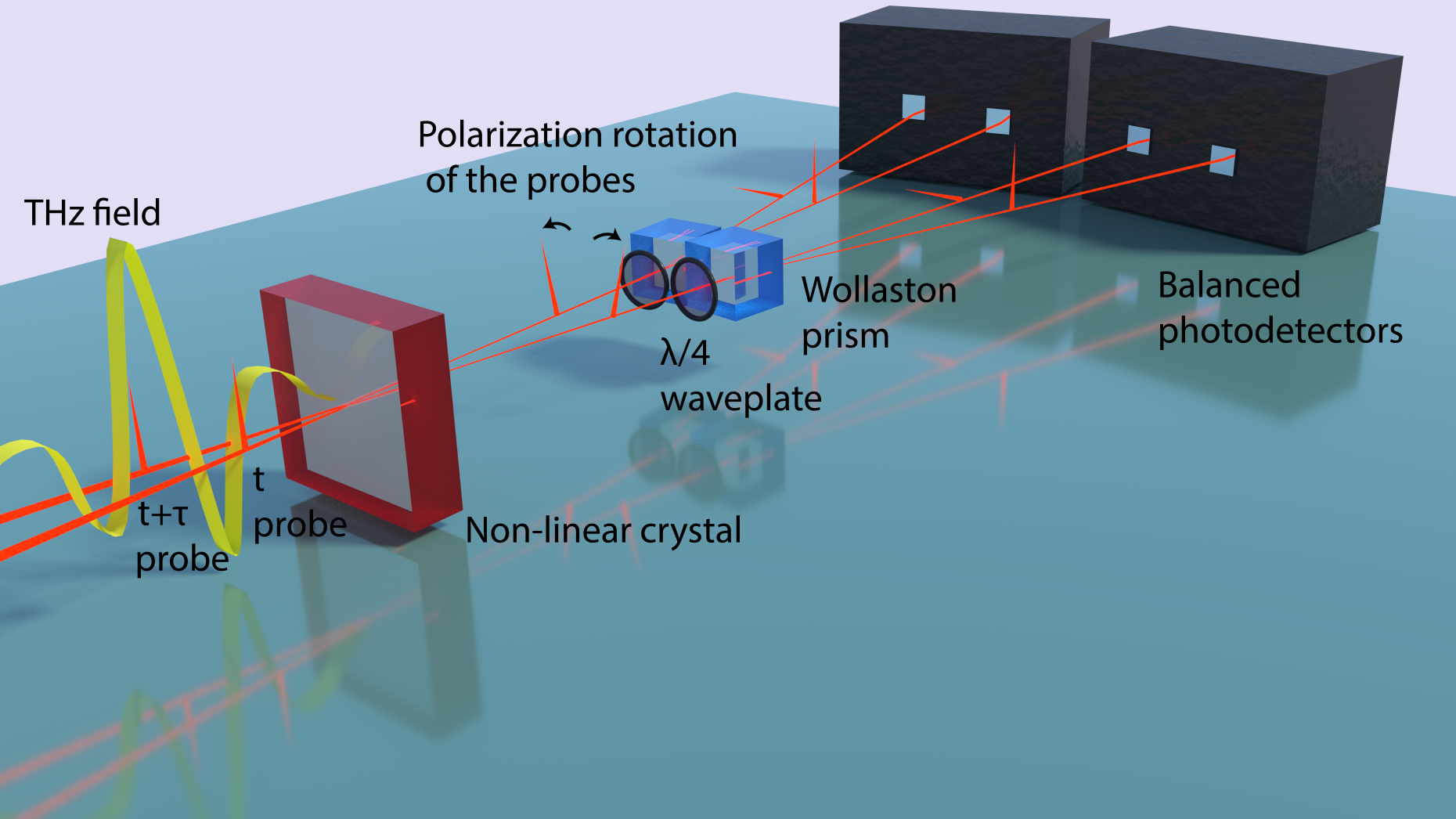
_{Figure 1: The additional probe polarization component induced onto each pulse via the non-linear interaction with the free running THz field can be measured directly through balanced detection configuration. The amplitude of the THz electric field is sampled at two space-time points with sub-cycle resolution in the nonlinear ZnTe crystal by two probe femtosecond pulses, mutually delayed by a time tau. The retrieved values of the electric field at time t and t+tau are then used for a real time computation of the correlation function thanks to a fast computation routine.}

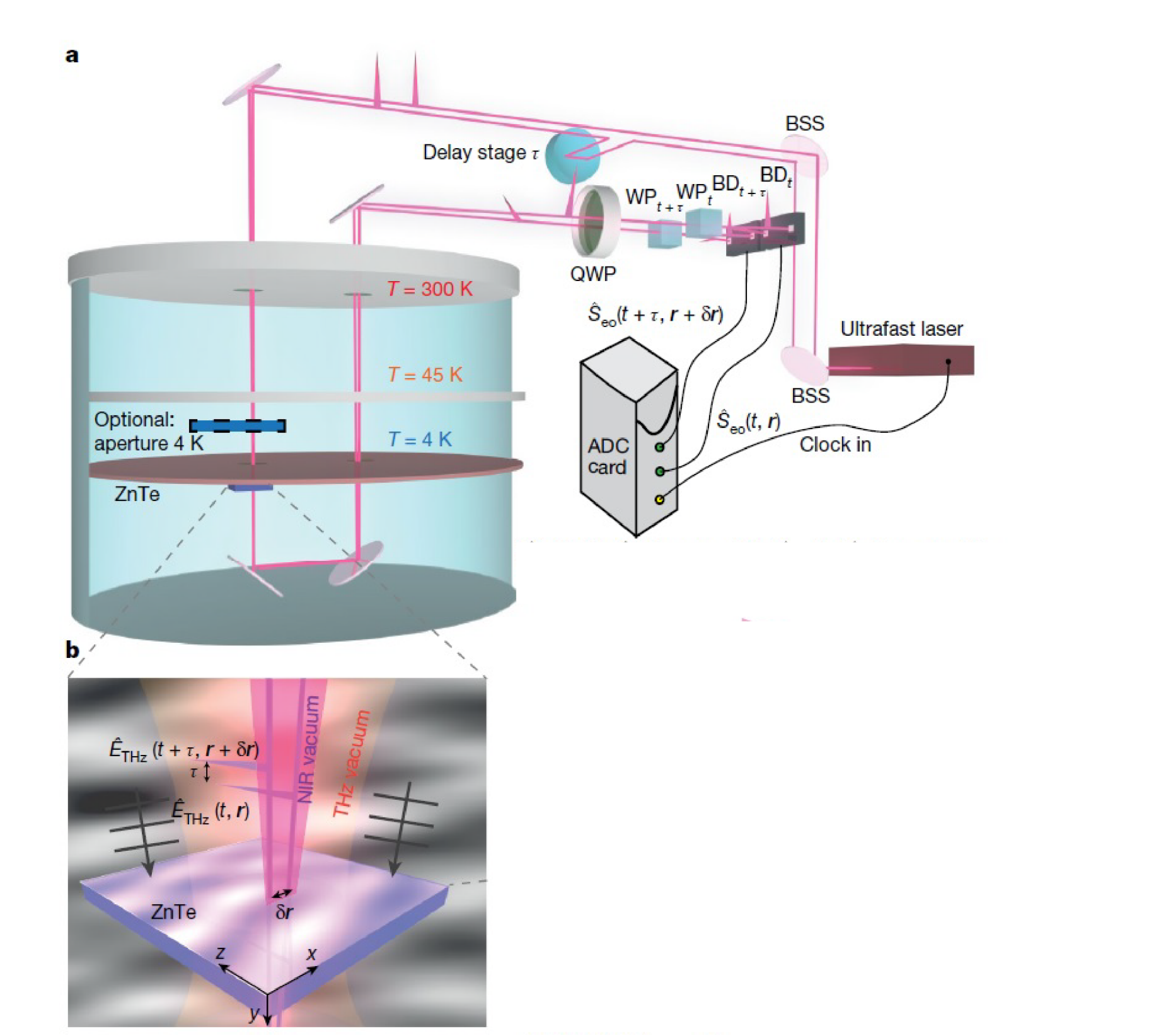
We implemented the two-point correlation measurement of \(G_{eo}(\tau, \delta\vec{r})\) using a pair of mode-matched 80-fs pulses of waist \( w_0 \) = 125 μm that sample the multimode THz vacuum field in the two space-time points as shown in Fig. 2a and in the zoom Fig. 2b. The detection crystal (a 3mm (110)-cut ZnTe) is inserted in a cryostat, which enables control of its thermal environment with temperatures between 4K and 300K and, as a consequence, of the mean photon occupation number of the thermal fields to which the crystal is exposed. The field-induced birefringence at two different space-time points is measured individually for each single probing pulse and separately for the two time-delayed trains of pulses with two balanced detection schemes, as represented in Fig.1.

_{Figure 2: a, Two probe pulses \( \small{E_p(t, \vec{r})}\) and  \( \small{E_p(t+\tau, \vec{r}+\delta\vec{r})}\) sample the electric field of the propagating waves in the crystal with the repetition rate of the laser used (80MHz). A mechanical delay stage provides a temporal delay of \( \tau\) to one of the probe pulses. The detection crystal (ZnTe, (110)-cut) is placed inside a closed-cycle cryostat and is thermally anchored to the 4K plate. It can be shielded from the blackbody radiation of the environment by two shields, with temperatures of 45K and 4K, respectively. The sampled electric fields introduce the electro-optic signals on the two probe pulses, which are individually recorded by means of an analogue-to- digital converter (ADC). Here, the relevant correlations are computed in real time. b, The vacuum field fluctuations couple from the environment into the detection crystal, where the multimode electric field \( \small{E_{THz}(t, \vec{r})}\) and \( \small{E_{THz}(t+\tau, \vec{r}+\delta\vec{r})}\)  is measured. An efficiently detected THz mode is composed of a superposition of plane waves that have favorable coherence properties with the probe beams. The lateral displacement of the pair of probe pulses \(\delta x\) is determined by an external mirror. This figure is taken from reference [1].}

The measured electro-optic field correlation \( G_{eo}(\tau, 0)\) is shown together with the associated power spectrum in Fig. 3 for two distinct temperatures, 300K and 4K. They are compared to the simulated results, obtained by summing the contribution to the signal of an infinity of (vacuum) electromagnetic modes propagating with arbitrary wave-vectors in a plane wave fashion [5] (See Fig 2b).

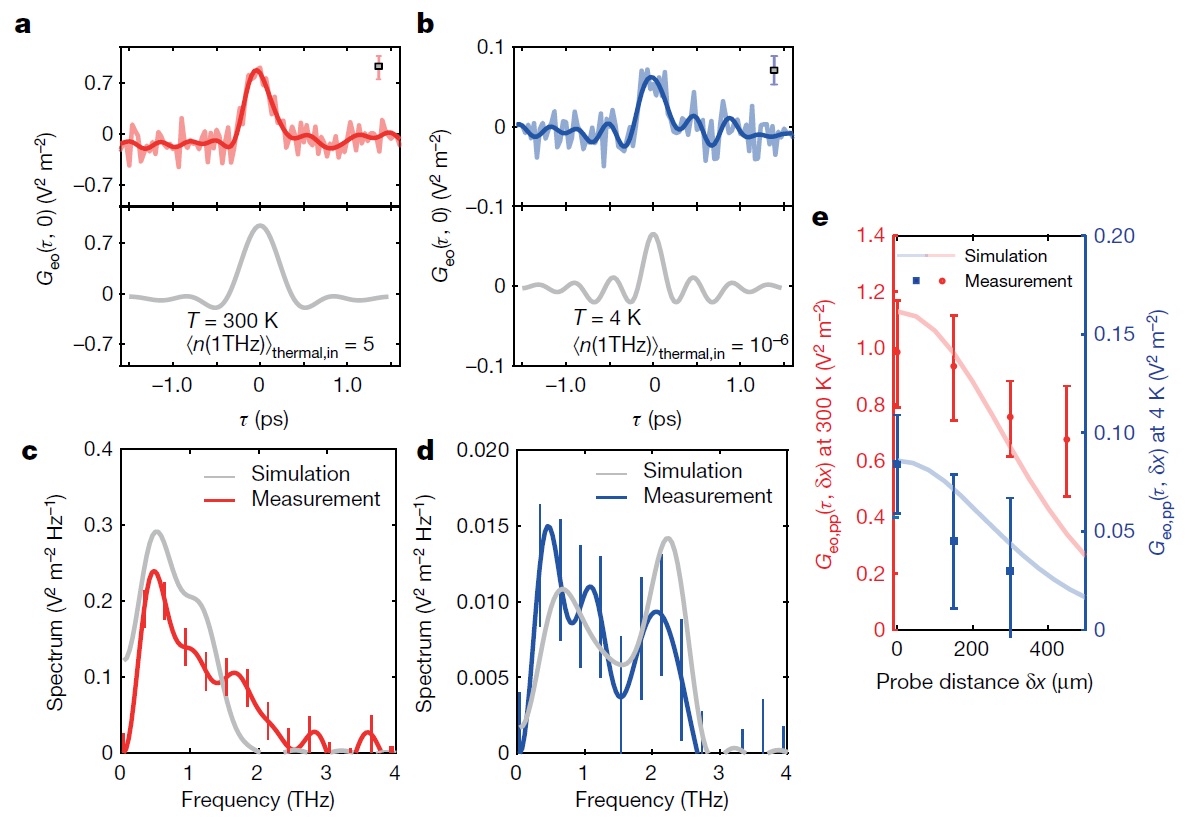
_{Figure 3: a, b, Electro-optic field correlation measurements \( \small{G_{eo}(\tau, 0)}\) (top plot) are compared to simulations (bottom plot) for two temperatures, 300K (a) and 4K (b). Faded lines denote raw measurements and thick lines the curves filtered by a low-pass Fourier filter with a cut-off frequency of 3THz, corresponding to the upper bound for efficient electro-optic detection in a 3-mm-thick crystal. c, d, The power spectra of the detected fields are estimated by computing the real part of the Fourier transform of the raw (unfiltered) electro-optic field correlations \(\small{G_{eo}(\tau, 0)}\), owing to the fact that, by definition, the electro-optic correlation function is symmetric around \(\small{\tau = 0}\). e, Spatial coherence of the probed vacuum (blue squares) and thermal fields (red dots). All error bars represent the 1σ confidence interval. This figure is taken from reference [1].}

In Fig. 3a and c, we show results obtained when the system is at T = 300K. In this condition, the blackbody radiation from the environment dominates over the vacuum field, with a photon occupation number of < \( n(\Omega = 2 \pi\times 1THz) \) > = 5. The field coherence is preserved for a duration of 250fs. The power spectrum reveals a large contribution of low-frequency components, which exhibit a high mean occupation of thermal photons. The contribution of high-frequency components is reduced by THz absorption in the detection crystal. The peak-to-peak signal is \( G^{(1)}_{eo,pp} = 0.98V^2m^{-2} \), and the root mean square of the noise is \( \sigma = 0.134V^2m^{-2} \).

In Fig. 3b and d, we show results when the system is at 4K base temperature (optional 4K aperture shown in Fig. 2a in use). In this condition, the trace and amplitude of the electro-optic field correlation change markedly, and the thermal contribution is suppressed (< \( n(\Omega = 2 \pi\times 1THz) \) > = 10^-6). The power spectrum of vacuum fluctuations contains frequency components in the frequency band around 0.75THz and around 2THz. This behaviour is well reproduced in our simulations and matches the coherence properties of the crystal. The peak-to-peak signal is \( G^{(1)}_{eo,pp} = 0.084V^2m^{-2} \), and the root mean square of the noise is \( \sigma = 0.018V^2m^{-2} \).

We additionally investigate the spatial electro-optic field correlation of the probed vacuum and thermal fields by displacing the two probe beams in the crystal along the x-axis, \(\delta\vec{r} = \delta x\vec{e}_x \). The lateral spatial coherence length of the probed multimode THz wave is determined by the participating waves with non-zero in-plane wavevector k⊥ and the transversal mode profile of the probe. In Fig. 3e, we report the peak-to-peak magnitude of \(G_{eo}(\tau, \delta x)\) as a function of the probe spacing \(\delta x \). We find that the spatial coherence is maintained over multiple wavelengths of the probed radiation, resulting in a lateral coherence length of 410μm at 300K and 375μm at 4K.

In recent experiments, we are analysing the dependence of the detection bandwidth on the probed space-time volume and exploring alternative measurement schemes. Amongst the most promising, a hybrid plasmonic-organic THz detection scheme integrated in silicon photonics [6] was demonstrated for efficient broadband THz field detection. It represents a highly sensitive room temperature electric field detector that holds promise for future quantum coherent interfaces at THz frequencies.