High-temperature devices

Quantum cascade lasers (QCLs) are promising candidates for compact, cheap, and efficient sources of terraherz (THz) radiation for a wide range of applications, such as imaging, spectroscopy, and telecommunication. In contrast to their mid-infrared counterparts, the THz QCLs could until recently only operate with cryogenic cooling, hindering a wide-sperad adoption outside of academic research. To this end, our group has been working towards reaching higher operation temperatures where thermoelectric cooling can be employed instead.

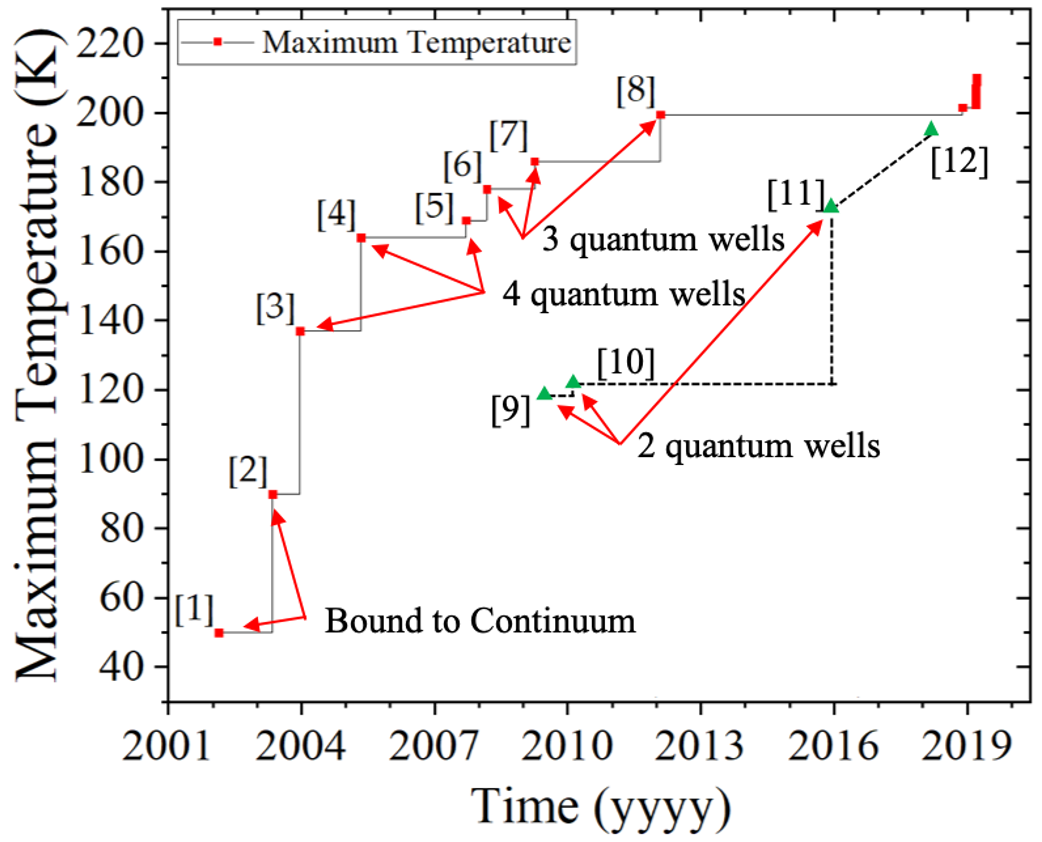
Our approach has been to follow the trend in THz QCL designs from their first realization in 2002 by Köhler et al.¹. As seen in Fig. 1, the maximum operating temperature has been increased as the number of wells in the active region period decreased^2–8, until in 2012 the so-called resonant phonon design based on three wells per period⁸ reached 199.5 K. At the same time, designs based on two quantum wells per period were investigated^9–12, but did not reach that high temperature due to their lower robustness to layer width changes.

*Fig. 1: Evolution of THz QCL design in terms of number of quantum wells per period and maximum operating temperature.*

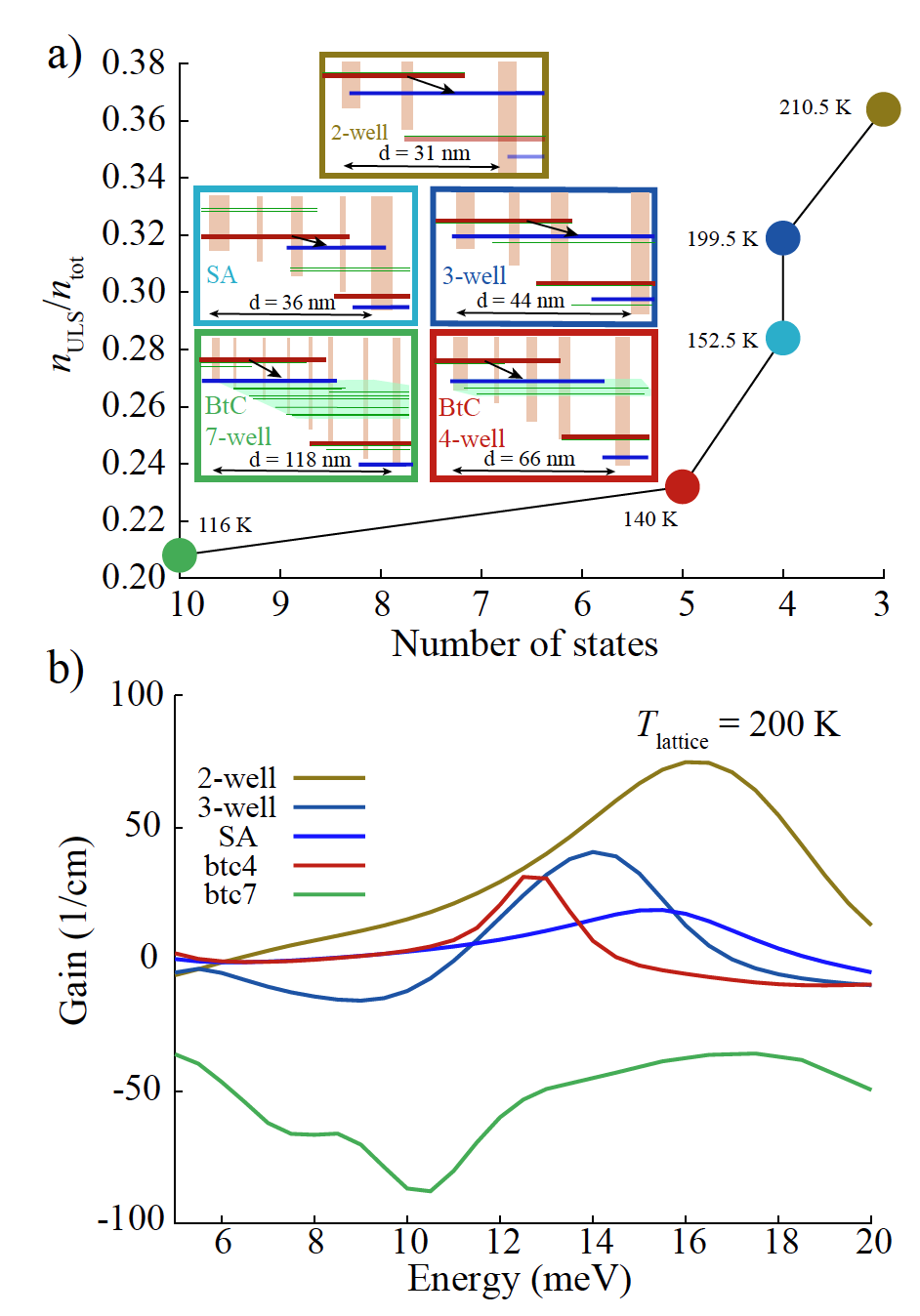
As shown in Fig.2, by simulating the best designs with various number of quantum wells per period, we see that fewer wells allows for a higher gain per period since fewer quantum levels are involved in the transport, and thus “steal” electrons from the upper laser level.¹³

To design new structures with improved performance, we used a nonequilibrium Green’s function (NEGF) model.¹⁴ This model is in general the most accurate and flexible one, but also computationally costly, why it has not been used for structure design and optimization in the past. However, owing to its accuracy, we could overcome the problem of layer width sensitivity and were able to lift the operating temperature close to the record value¹⁵, and then later set a new record temperature value¹³. Fig. 3 summarizes the simulations and experimental results for this record device, which had a high enough temperature to be operated on a multistage thermoelectric cooler.

Fig. 3: a) States and electron density at 200 K of the 2-well QCL. b) Peltier-cooled laser performance. c) T0 fit of the threshold current and the QCL box with Peltier cell. d) First cryo-free THz QCL spectra. Reprinted from Ref. 13 with permission.

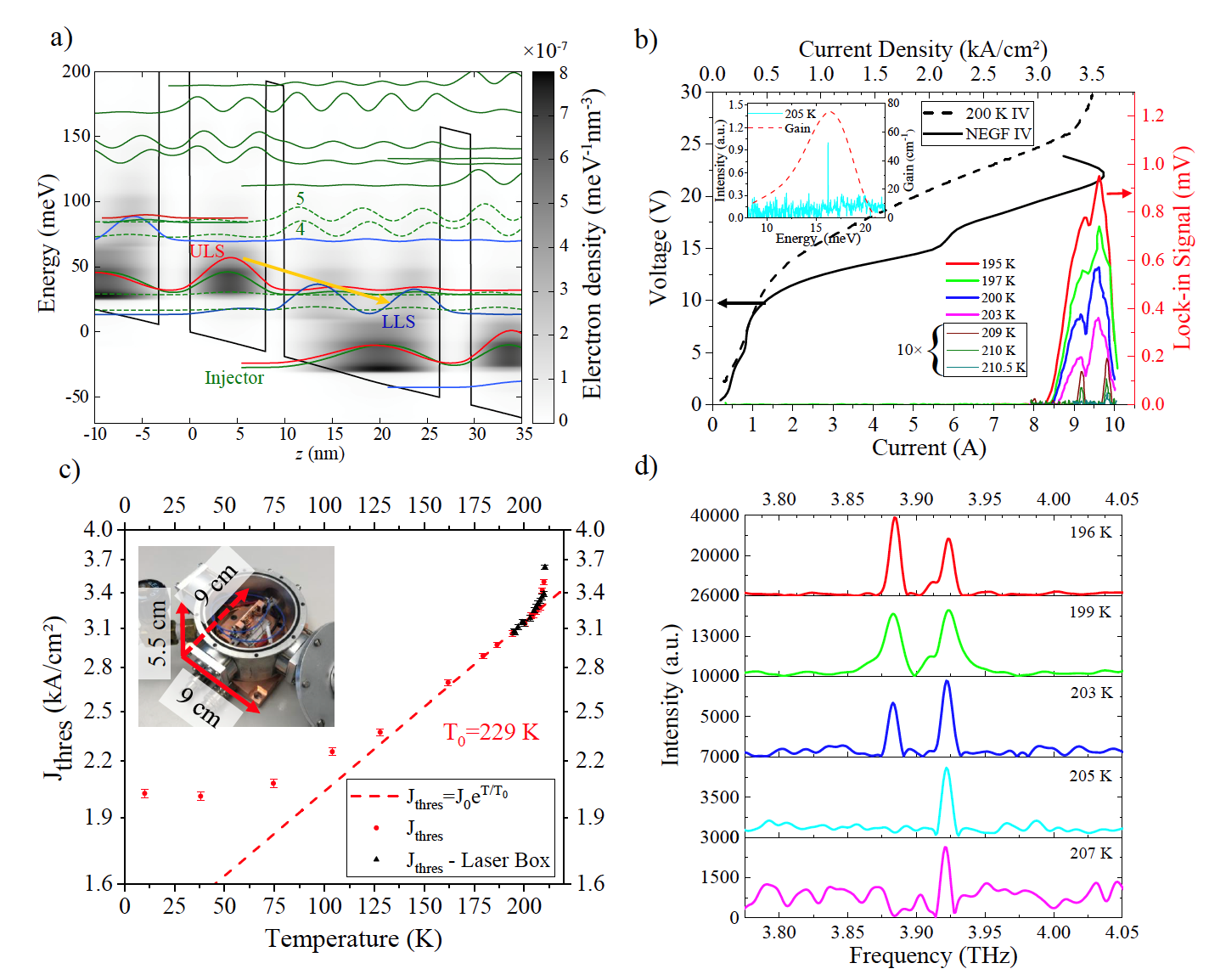
In order to reach high operating temperatures, not only the gain of the active region has to be maximized, but also the losses of the wave guide have to be minimized. Therefore, a significant effort was put into fabricating Cu-Cu double-metal wave guiding instead of the usual Au-Au process, as well as to grow thicker active regions than usual.

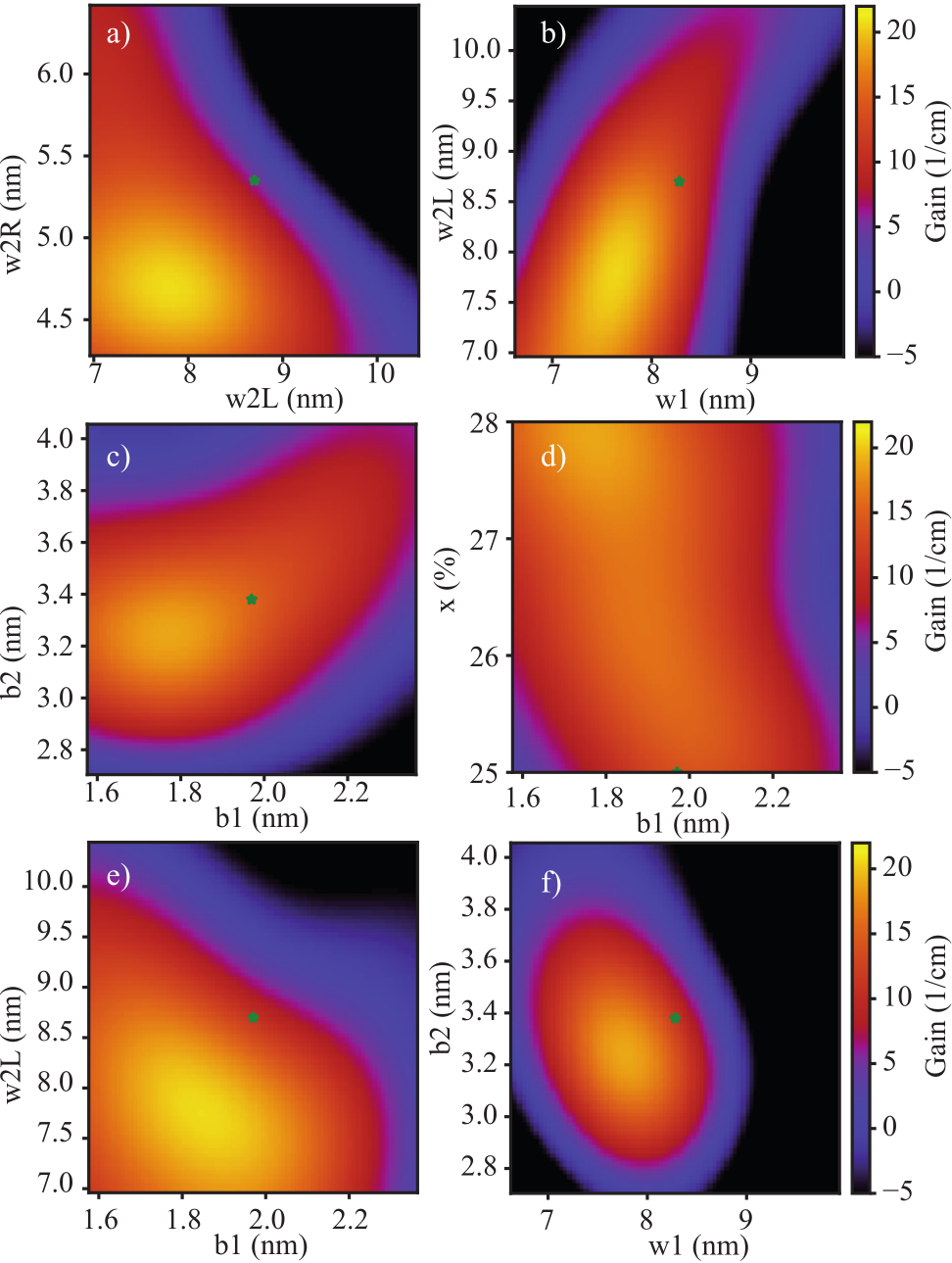
The design of this record-performing laser was obtained by a systematic optimization of the previous design using the NEGF model.¹⁶ Encouraged by the good performance of the laser, we have continued to optimize this design by varying even more parameters of the structure. For this, all layers were varied continuously, as well as the AlAs composition (x) of the barriers, which determines the conduction band offset. The evaluation of a structure was performed in two steps, first computing the current-voltage characteristics, and then computing the gain spectrum at the bias of highest current, where these lasers normally has their highest gain (before negative differential resistance sets in). Since one such evaluation would take many days to complete, the simulations were performed on the Euler computer cluster at ETH Zürich, and a new optimization algorithm based on machine learning and Bayesian regression was developed in order to greatly accelerate the convergence rate (see Fig. 4).

Fig. 4: Comparing generic algorithm (GA), 1D information algorithm with parallel trials (IAPT), and Gaussian process (GP) optimization for a 2-well QCL (average of 100 optimizations). Repr. from Ref. 16 with permission.

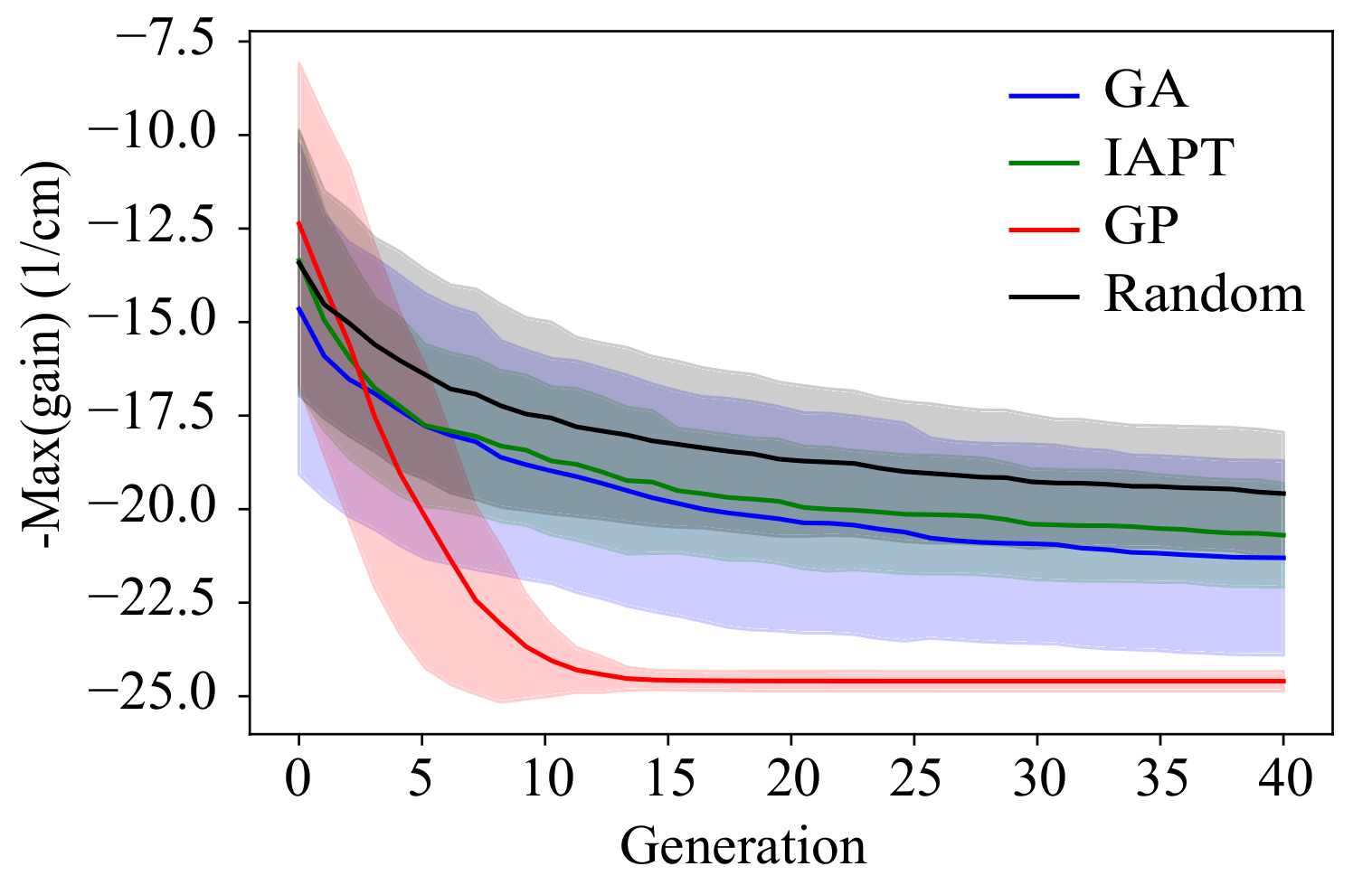
Using this optimization scheme, the gain was evaluated for several hundred structures and the gain could be increased from 14 cm^-1 to 20 cm^-1 at room temperature (including electron-electron scattering), which is barely enough to overcome the total optical losses. By fitting the gain of all the computed structures using Bayesian regression, we obtain the 2D plots shown in Fig. 5, which reveal the important parameters. In summary, a high conduction band offset as possible, a narrow extraction well with an extraction energy (E_ex=51 meV) much larger than the optical phonon energy (E_LO = 36 meV), and a laser barrier giving a normalized oscillator strength around 0.20 gives the optimal performance.

Fig 5 — Fig. 5: Gain dependence of the two-well-QCL scheme on pairs of parameters. The green asterisks indicate the nominal-design parameters. The labels are defined in Fig. 1(a) of Ref.16. Reprinted from Ref. 16 with permission from the authors.

References

1. Köhler, R. et al. Terahertz Semiconductor-Heterostructure Laser. Nature 417, 156 (2002).
2. Scalari, G. et al. Far-infrared (λ≃87 μm) bound-to-continuum quantum-cascade lasers operating up to 90 K. Appl. Phys. Lett. 82, 3165–3167 (2003).
3. Williams, B. S., Kumar, S., Callebaut, H., Hu, Q. & Reno, J. L. Terahertz quantum-cascade laser operating up to 137 K. Appl Phys Lett 83, 5142 (2003).
4. Williams, B. S., Kumar, S., Hu, Q. & Reno, J. L. Operation of terahertz quantum-cascade lasers at 164 K in pulsed mode and at 117 K in continuous-wave mode. Opt. Express 13, 3331–3339 (2005).
5. Kumar, S. et al. Terahertz quantumcascade lasers with resonantphonon depopulation: hightemperature and lowfrequency operation. in Proceedings of The Ninth International Conference on Intersubband Transitions in Quantum Wells T16 (2007).
6. Belkin, M. A. et al. Terahertz quantum cascade lasers with copper metal-metal waveguides operating up to 178 K. Opt Express 16, 3242–3248 (2008).
7. Kumar, S., Hu, Q. & Reno, J. L. 186 K operation of terahertz quantum-cascade lasers based on a diagonal design. Appl. Phys. Lett. 94, 131105 (2009).
8. Fathololoumi, S. et al. Terahertz quantum cascade lasers operating up to ∼ 200 K with optimized oscillator strength and improved injection tunneling. Opt. Express 20, 3866–3876 (2012).
9. Kumar, S., Chan, C. W. I., Hu, Q. & Reno, J. L. Two-well terahertz quantum-cascade laser with direct intrawell-phonon depopulation. Appl. Phys. Lett. 95, 141110 (2009).
10. Scalari, G. et al. Broadband THz lasing from a photon-phonon quantum cascade structure. Opt. Express 18, 8043 (2010).
11. Albo, A., Flores, Y. V., Hu, Q. & Reno, J. L. Two-well terahertz quantum cascade lasers with suppressed carrier leakage. Appl. Phys. Lett. 111, 111107 (2017).
12. Franckié, M. et al. Two-well quantum cascade laser optimization by non-equilibrium Green’s function modelling. Appl. Phys. Lett. 112, 021104 (2018).
13. Bosco, L. et al. Thermoelectrically cooled THz quantum cascade laser operating up to 210 K. Appl. Phys. Lett. 115, 010601 (2019).
14. Wacker, A., Lindskog, M. & Winge, D. O. Nonequilibrium Green’s Function Model for Simulation of Quantum Cascade Laser Devices Under Operating Conditions. Sel. Top. Quantum Electron. IEEE J. Of 19, 1200611 (2013).
15. Franckié, M. et al. Two-well quantum cascade laser optimization by non-equilibrium Green’s function modelling. Appl. Phys. Lett. 112, 021104 (2018).
16. Franckié, M. & Faist, J. Bayesian Optimization of Terahertz Quantum Cascade Lasers. Phys. Rev. Appl. 13, 034025 (2020).