Optically Probed Polaritons
In optically probed experiment, we observe the evolution of the sample transmission as a function of the applied magnetic field (normalized to the electric field of the reference 2DEG wafer at B=0). As the magnetic field is swept a profound modification of the sample transmission is observed. The possibility to tune in a continuous way the material excitation allows to follow the evolution of polaritonic states as the system is driven from the uncoupled regime to the strongly coupled one.
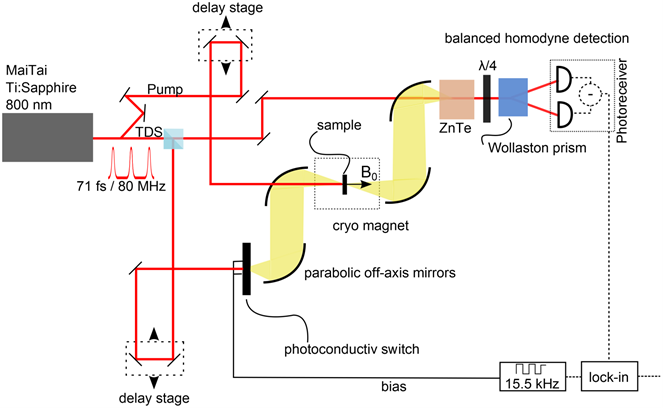
The samples are investigated using a transmission spectrometer based on a THz-Time Domain Spectroscopy (TDS) setup coupled to a liquid helium cryostat equipped with a superconducting magnet (maximum field of 11T) and a variable temperature insert (1.9-300°K). The scheme of the setup with the essential components is displayed in Fig. 1.
Figure 1: Experimental setup used for the transmission experiments. The ultrafast Ti:sapphire laser of pulse width < 75fs illuminates a photoconductive switch producing a broadband THz pulse of length 2ps The THz pulse propagates parallel to the DC magnetic field direction in order couple to the cyclotron transition of the 2DEG. THz-TDS allows coherent detection of the amplitude and phase of the THz electric field. The figure is taken from ref 1.
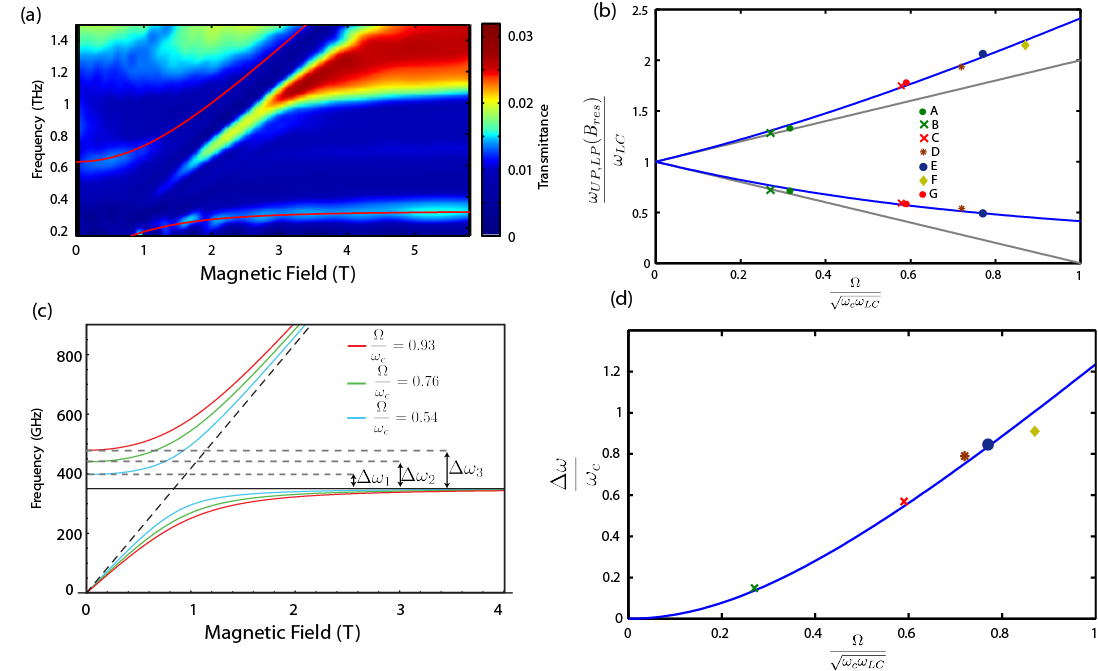
We leveraged on this experimental arrangement and we demonstrated record-high coupling ratios up to 0.87 (Fig. 2a), ultrastrong coupling with superconducting cavities (NJP) and electrically tunable ultrastrong coupling. We were able to identify peculiar behavior of ultrastrongly coupled systems as illustrated in Fig. 2b,c,d2
Figure 2: (a)Transmission through sample with Nb resonator with the LC-mode at 310 GHz. (b)The evolution of the normalized polariton frequencies at resonance follows clearly the blue shifted prediction (in blue). The gray lines show the linear behavior expected in the strong coupling regime (without diamagnetic and counter-rotating terms). (c) Calculated polariton branches as a function of the coupling strength for a resonator frequency of 350 GHz. (d) Normalized polaritonic gap as function of the normalized coupling ratio. The figure is taken from ref 2.
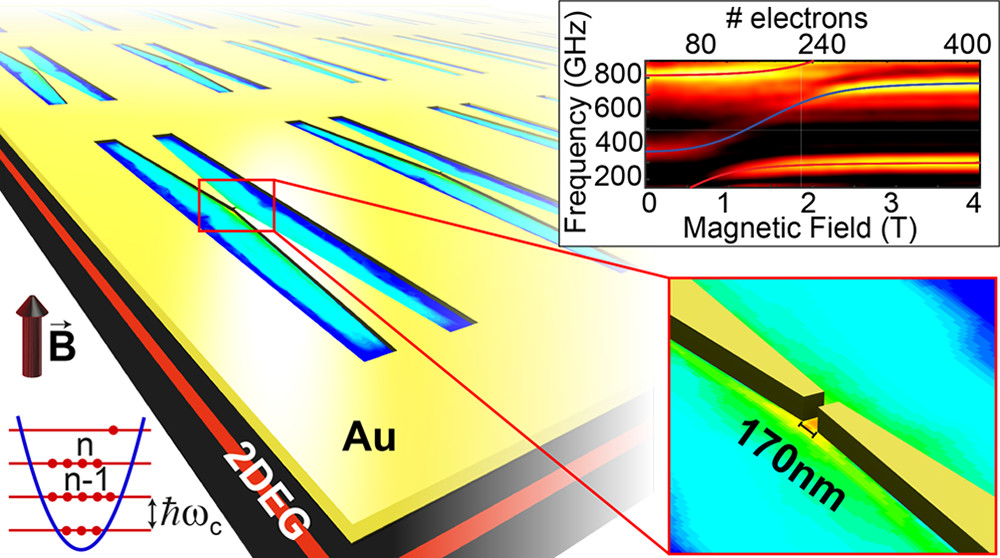
By using hybrid dipole antenna-split ring resonator-based cavities (Fig. 3) with extremely small effective mode volumes \( \frac{V_{eff}}{\lambda_0^3} \approx 6 \times 10^{-6} \) and surfaces \( \frac{S_{eff}}{\lambda_0^2} \approx 3.5 \times 10^{-6} \), we probe the ultrastrong light-matter coupling at 300GHz to less than 100 electrons located in the last occupied Landau level of a high mobility
two-dimensional electron gas, measuring a normalized coupling ratio of \( \frac{\Omega_R}{\omega} = 0.36\)3. Effects of the extremely reduced cavity dimensions are observed as the light-matter coupled system is better described by an effective mass heavier than the uncoupled one. These results open the way to ultrastrong coupling at the single-electron level in two-dimensional electron systems.
Figure 3: Schematic of a hybrid dipole antenna-split ring resonator-based cavity(left) with the in-plane electric field E that couples with the TE polarized Inter-Landau-level transition (calculated with 3D finite element solver). The colorplot (top-right) shows the transmission of the coupled system as a function of the magnetic field together with the corresponding polaritonic branches experimentally measured. The number on the top x- axis shows the number of electrons coupled to the first mode of the cavity at each magnetic field. The figure is taken from ref 3.
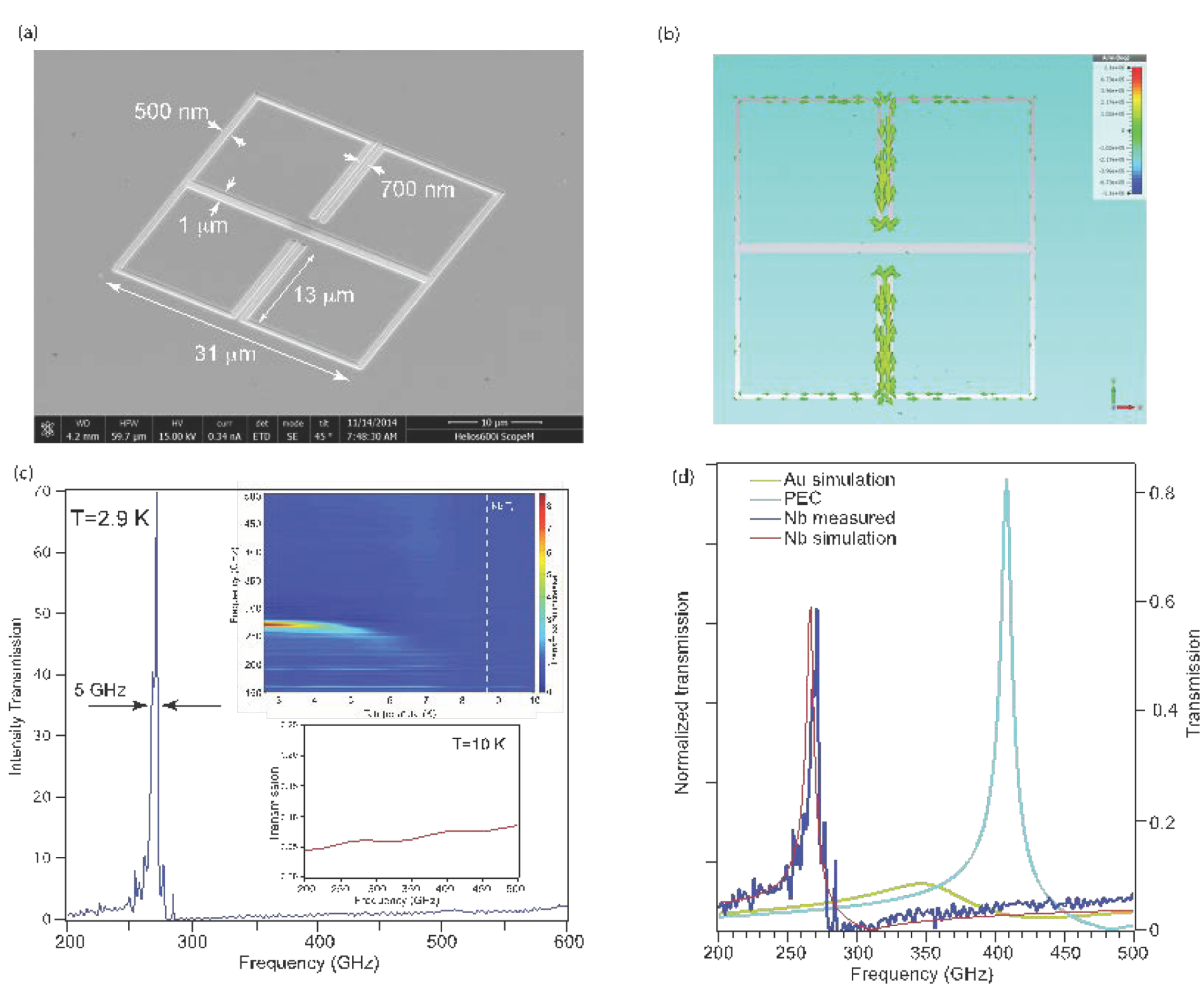
The possibility to modulate the ultrastrong coupling regime by changing the characteristics of the cavity can be implemented by using superconducting resonators with high switching capabilities. To maximize the switching effect allowed by the presence of the superconductor, we adopted the following design strategy: we increased the radiative Q factor in order to have a structure whose resonance line width is loss limited. The radiative quality factor can be engineered by acting on the capacitor gap dimension in order to reduce the efficiency of the dipolar coupling as well as the inter-meta-atom spacing . An SEM picture of the fabricated metasurface is reported in Fig. 4a together with 3D simulations of the surface currents. Measurements of the metasurface reported in Fig. 4c yield a quality factor Q=54 increasing by a factor of 10 the usual quality factor of split-ring resonators4.
Figure 4: (a) SEM picture of one meta-atom constituting the complementary Nb metasurface (100 nm thick film). (b) finite element 3D simulation of the currents flowing in the meta-atom for the Nb in the superconducting state. The highest current density is in the long and narrow wires.(c) Metasurface intensity transmission at T=2.6K normalised to the transmission value at T=10K for a long scan of 40mm. Inset (high) color plot of the metasurface amplitude transmission as a function of the temperature, normalised to the transmission at 10K. Inset (low) Metasurface transmission at 10K referenced to empty sample holder, no resonance is observed (d) Experimental transmission at 2.6K normalized to transmission at 10K for the Nb metasurface (blue line, left y-axis) together with simulated curve for the same quantity (red line, left y-axis). Simulated transmission for Perfect Electric Conductor (light blue line, right y-axis) and Gold (yellow line, right y-axis). The figure is taken from ref 4.
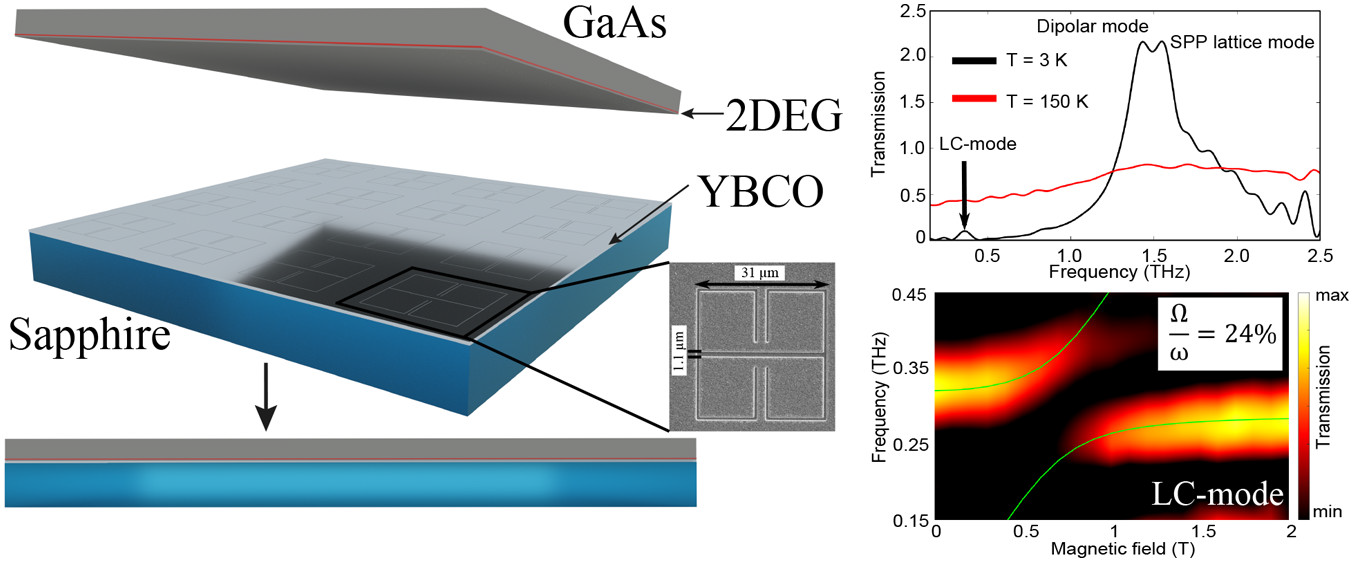
Using superconducting metasurfaces was continued by fabricating high temperature superconducting metasurfaces from yttrium−barium−copper oxide (YBCO) films via focused ion beam milling. The design of the complementary split ring resonators yields a high quality factor (up to Q = 31) resonance, which is fully switchable when exploiting the transition from the superconducting to normal conducting state, which is achieved by heating the sample above the critical temperature. Meanwhile, the resonance is continuously visible and frequency stable under the action of a magnetic field, up to B = 9T. This makes it an ideal candidate for light−matter coupling experiments with magnetic field tunable Landau level transitions. We presented two techniques to bring the metasurface in close vicinity of a 2D electron gas in an AlGaAs/GaAs QW without direct deposition, and we achieve a normalized vacuum Rabi frequency of \( \frac{\Omega_R}{\omega} = 0.24 \)5.
Figure 5: Sketch of the sample assembly, placing the 2DEG on top of the resonators in which the stack is then held by two metal plates which are screwed together (Left). There is also a scanning electron micrograph (SEM) of one resonator with indicated dimensions. (Top- right) Transmission spectra of the resonator array at T = 150°K and T = 3°K, both normalized to the transmission at T = 220°K. (Bottom-right) Transmission spectra as a function of magnetic field showing an anticrossing of the LC mode of the resonator with a normalized coupling strength of \( \small{\frac{\Omega_R}{\omega} = 0.24 }\). The figure is taken from ref 5.
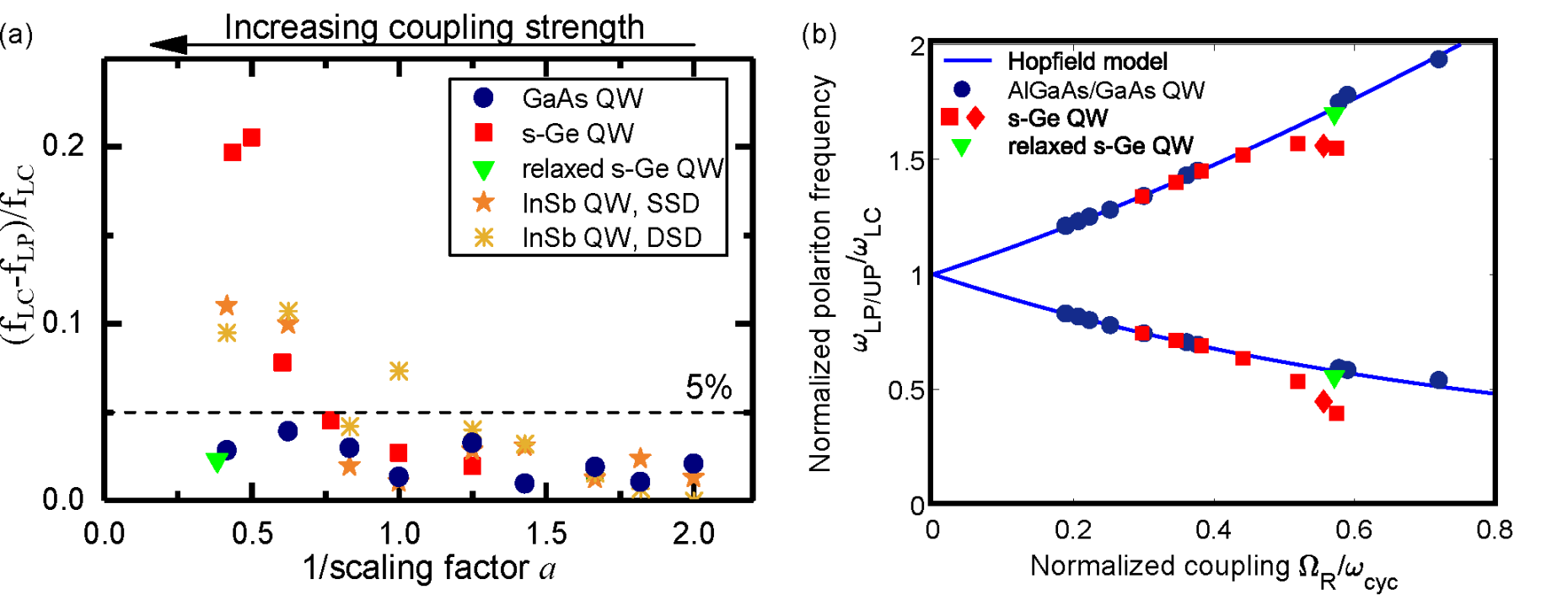
We also probed ultrastrong light-matter coupling between metallic terahertz metasurfaces and Landau-level transitions in other high-mobility two-dimensional electron and hole gases. We utilized heavy-hole cyclotron resonances in strained Ge and electron cyclotron resonances in InSb quantum wells, both within highly nonparabolic bands, and compared our results to well-known parabolic AlGaAs/GaAs quantum well systems. Tuning the coupling strength of the system by two methods, lithographically and by optical pumping, we observed a behavior clearly deviating from the standard Hopfield model previously verified in cavity quantum electrodynamics: an opening of a lower polaritonic gap6.
Figure 6: (a) The deviation of the lower polariton frequency \(\small{f_{LP}}\) to the cold cavity frequency \(\small{f_{LP}}\) is displayed for a GaAs QW (dark blue circles), a s-Ge QW (red squares), and InSb QWs [orange (single-side-doped QW) and yellow (double-side-doped QW) stars] as a function of the geometrical scaling, where the coupling strength increases towards the left. (b) Normalized polariton frequencies \( \small{\frac{\Omega_{LP/UP}}{\omega_{LC}}} \) at the position of minimal splitting versus the normalized coupling strength \(\small{\frac{\Omega_{R}}{\omega_{cyc}}}\). The theoretical Hopfield model is displayed by blue solid lines. Experimental data points for parabolic 2D electrons in GaAs QWs fit the Hopfield model (dark blue circles). Experimental data points for the nonparabolic 2D heavy holes in a s-Ge QW are displayed by red squares (series 1) and diamonds (series 2). The bright green triangles are for a partially relaxed s-Ge QW of sample series 2. The figure is taken from ref 6.
References
1 Scalari, G.; Maissen, C.; Cibella, S.; Leoni, R.; Reichl, C.; Wegscheider, W.; Beck, M.;Faist, J. THz ultrastrong light-matter coupling. 2016.
2 Maissen, C.; Scalari, G.; Valmorra, F.; Beck, M.; Faist, J.; Cibella, S.; Leoni, R.; Re-ichl, C.; Charpentier, C.; Wegscheider, W. Ultrastrong coupling in the near field ofcomplementary split-ring resonators. Phys. Rev. B 2014, 90, 205309.
3 Keller, J.; Scalari, G.; Cibella, S.; Maissen, C.; Appugliese, F.; Giovine, E.; Leoni, R.;Beck, M.; Faist, J. Few-Electron Ultrastrong Light-Matter Coupling at 300 GHz withNanogap Hybrid LC Microcavities. Nano Letters 2017, 17, 7410–7415.
4 Scalari, G.; Maissen, C.; Cibella, S.; Leoni, R.; Faist, J. High quality factor, fully switch-able terahertz superconducting metasurface.Applied Physics Letters 2014, 105, 261104.
5 Keller, J.; Scalari, G.; Appugliese, F.; Mavrona, E.; Rajabali, S.; Süess, M. J.; Beck, M.;Faist, J. High Tc Superconducting THz Metamaterial for Ultrastrong Coupling in a Magnetic Field. ACS Photonics 2018, 5, 3977–3983.
6 Keller, J.; Scalari, G.; Appugliese, F.; Rajabali, S.; Beck, M.; Haase, J.; Lehner, C. A.;Wegscheider, W.; Failla, M.; Myronov, M.; Leadley, D. R.; Lloyd-Hughes, J.; Nataf, P.;Faist, J. Landau polaritons in highly nonparabolic two-dimensional gases in the ultra-strong coupling regime.Phys. Rev. B2020,101, 075301.