Ultrastrong Light-Matter coupling Tutorial

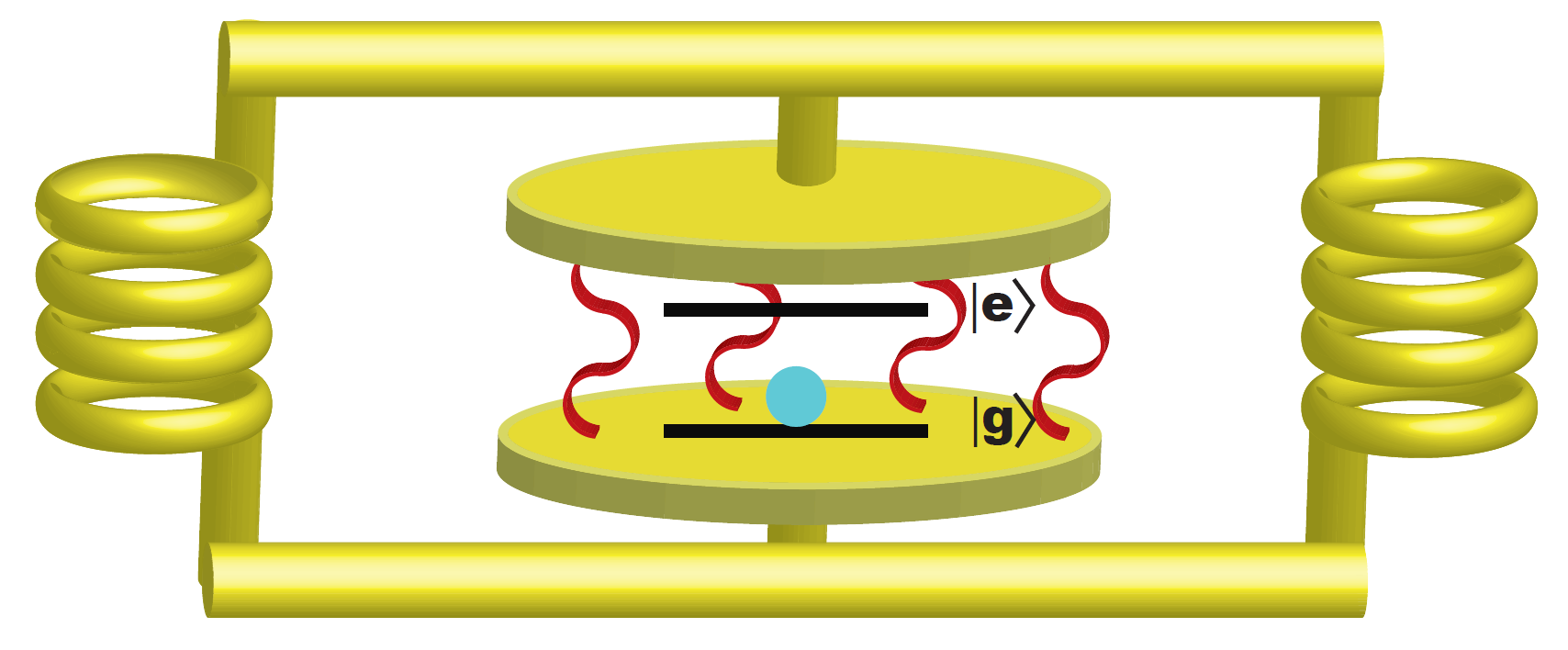
The interaction Hamiltonian (minimal coupling, the vector potential \(\vec{A}\) is the one for the single mode cavity) can be written as:

\begin{equation}
\frac{1}{2 m_e}(\vec{p}-e\vec{A})^2=\frac{1}{2 m_e} ({p}^2-\vec{p}\cdot\vec{A}-\vec{A}\cdot\vec{p}+{A}^2)\\
\end{equation}

with a convenient gauge choice

\begin{eqnarray*}
\vec{p}\rightarrow -i\hbar \nabla\\
\nabla \vec{A}=0 \rightarrow [\vec{A},\vec{p}]=0\\
\frac{1}{2 m_e} ({p}^2-2\vec{p}\cdot\vec{A}+{A}^2) \rightarrow
\frac{1}{2 m_e}{p}^2-\frac{1}{ m_e}\vec{p}\cdot\vec{A}+\frac{1}{2 m_e}{A}^2
\end{eqnarray*}

The role of the \(A^2\) and of the counter rotating terms is central in the ultrastrong light matter coupling. These terms are usually neglected when the interaction is not so strong, in other words when their expectation value on the ground state is small with the respect to the two-level system energy. If we express the coupling energy as \(\hbar\Omega_R\), the normalized light-matter coupling ratio can be written as \(\frac{\Omega_R}{\omega_0}\). This is the relevant figure that quantifies the different light-matter coupling regimes

Strong coupling: Jaynes-Cummings Hamiltonian

A single two-level system coupled to a single mode cavity in the rotating-wave approximation and neglecting \(A^2\) terms (i.e. when \(\frac{\Omega_R}{\omega_0}\ll 1\)) is described by the so-called Jaynes-Cummings³ Hamiltonian.

\begin{equation}
\hat{\mathcal{H}}_{JC}=\hbar \omega_c \hat{a}^{\dagger}\hat{a}+\hbar\omega_0 \hat{\sigma}_z +\hbar g(\hat{\sigma}^{\dagger}\hat{a}+\hat{\sigma}\hat{a}^{\dagger})
\end{equation}

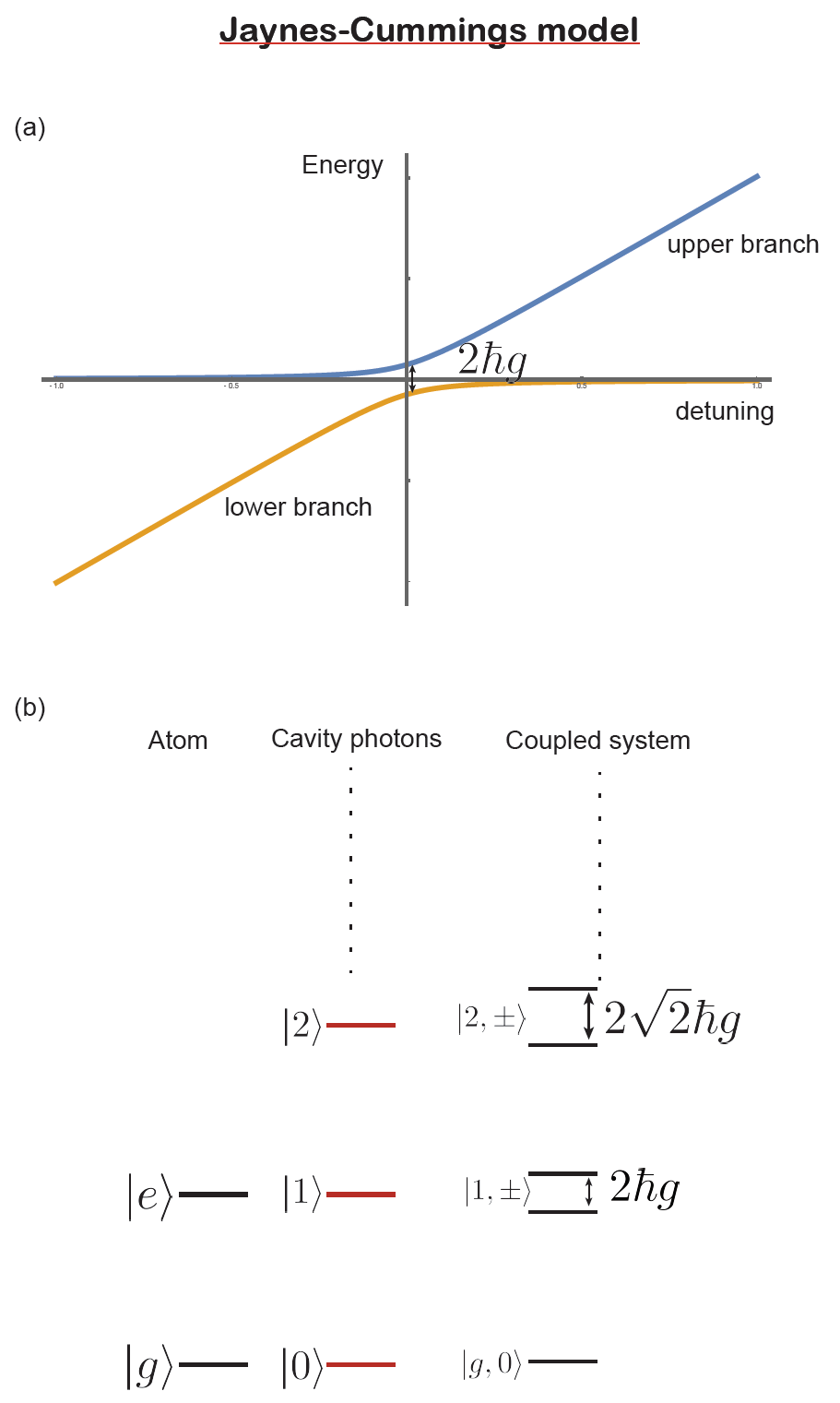
The main results are the emergence of mixed light-matter coupled states called cavity polaritons: the energy spectrum of the coupled system (at resonance \(\omega_c=\omega_0\)) features a non-linearity in energy spacing proportional to the square root of the number of photons \(n\):

\begin{equation}
E(n,\omega)=\hbar\omega_c\left(n+\frac{1}{2}\right)\pm\hbar 2g\sqrt{n+1}
\end{equation}

The level are split and their energy dispersions are called polariton branches. The energy states constitute the Jaynes-Cummings ladder.

Ultrastrong coupling: Dicke and Hopfield Hamiltonians

When the light-matter coupling becomes comparable to the unperturbed energy levels (i.e. when \(\frac{\Omega_R}{\omega_0} \leq 1\) or even \(\frac{\Omega_R}{\omega_0} > 1\)) the counter-rotating and \(A^2\) terms must be included in the Hamiltonian⁴. Two-level systems physics in the presence of strong interactions and counter-rotating terms was already investigated by Bloch and Siegert on spin systems⁵. If we inspect the generic expression for the Rabi energy for a system of N identical two-level systems with dipole \(d\) coupled to the same photonic mode with a volume \(V_{cav}\):

\begin{equation}
\hbar \Omega_R \propto d\sqrt{N} E_{vac} =d\sqrt{N} \sqrt{\frac{\hbar \omega}{\epsilon V_{cav}}}
\end{equation}

We see that its magnitude can be increased by increasing N and/or by decreasing the cavity volume \(V_{cav}\) that will affect the magnitude of the vacuum field fluctuations. The problem of coupling \(N)two-level systems to the same spatial mode was first discussed by Dicke in his seminal work about superradiance⁶ within the rotating wave approximation. Among his findings, there is the fundamental fact that the interaction scales with the \(\sqrt{N}\).
In order to account for arbitrary strength of light-matter coupling in the case of $N$ two level systems coupled to the same photonic mode, the Hopfield Hamiltonian⁷ must be used. It basically consists of the Dicke Hamiltonian⁶ including counter-rotating and \(A^2\) terms.
The general formulation is the following (see for example⁸):

\begin{equation}
\hat{\mathcal{H}}_{Hop}= \hbar \omega_c \hat{a}^{\dagger}\hat{a}+\hbar\omega_0 \left(\hat{b}^\dagger\hat{b}-\frac{N}{2}\right) +\hbar \frac{\Omega_R}{\sqrt{N}}(\hat{a}^{\dagger}+\hat{a})(\hat{J}_{-}+\hat{J}_{+})+D(\hat{a}^{\dagger}+\hat{a})^2
\end{equation}

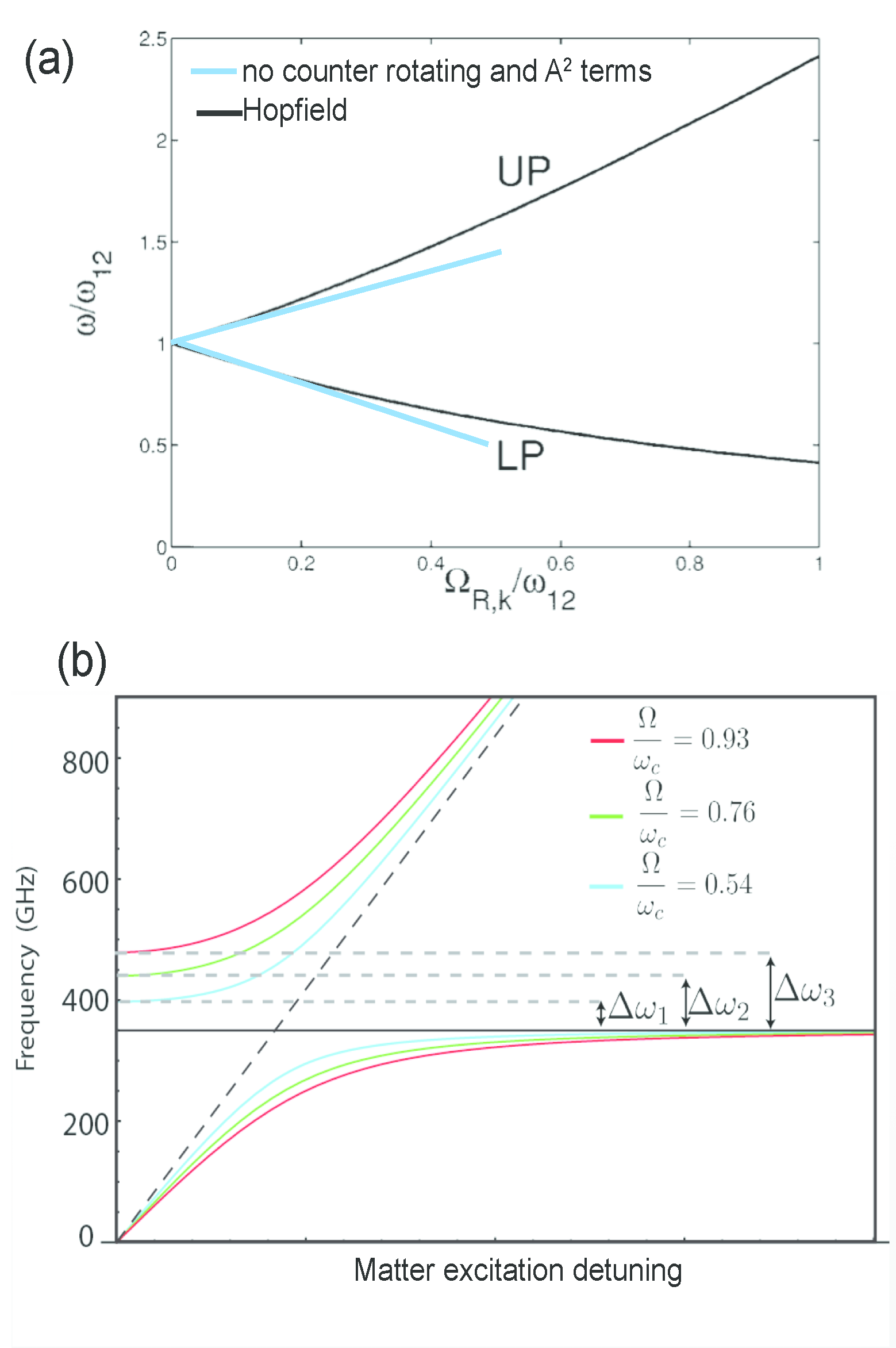
This general formulation can then be applied to a variety of platforms where ultrastrong light-matter coupling has been implemented⁹, from circuit QED in the microwaves to organic molecules in the visible. when \(N\) oscillators are considered, the light-matter coupled system loses some important quantum optical features (i.e. the non-linearity in the photon number \(\sqrt{n}\)) but acquires other important and exotic properties. As there is not a threshold (like in a phase transition) the ultrastrong coupling regime can be defined when some specific signatures start to be observable. The deviation of the polaritonic from the linear dispersion as a function of the coupling strength Fig. 3(a), the opening of a polaritonic gap¹⁰ Fig. 3(b) (completely analogous to the reststrahlen band in phonon polaritons) and the normalized ratio \(\frac{\Omega_R}{\omega_0}\geq 0.1\)¹¹ are usually considered as benchmarks in experimental realizations.

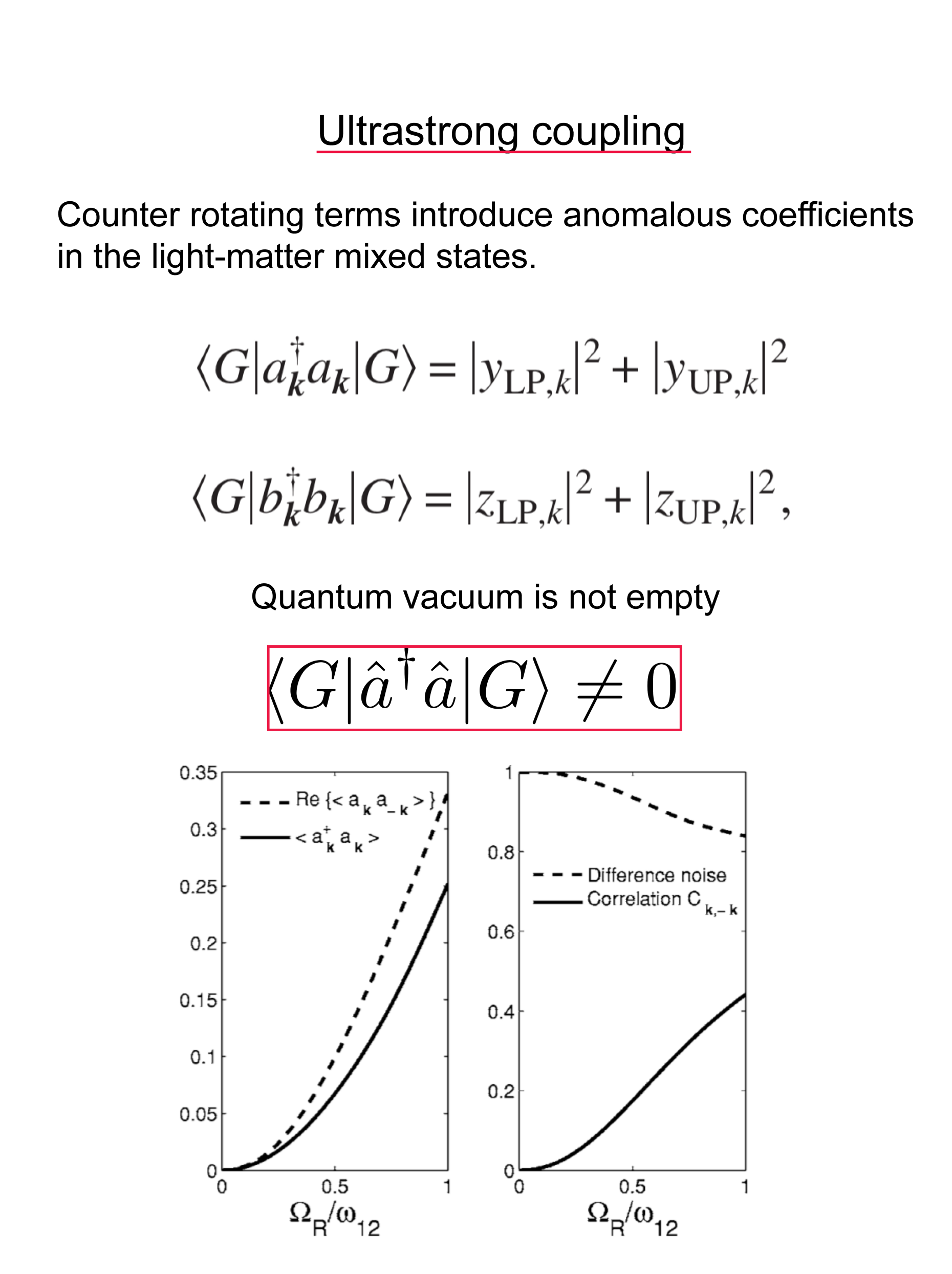
Among many interesting aspects and theoretical predictions, the ultrastrong coupling regime features the presence of virtual photons in the ground state. As visible in Fig.4 the expectation value of matter excitations (\(\hat{b}^{\dagger}\hat{b}\)) and photon number (\(\hat{a}^{\dagger}\hat{a}\)) is non-zero in the ultrastrong coupling: the inclusion of counter rotating terms mixes light matter operators giving rise to a polariton vacuum that is populated by excitations. The ground state photon population and their correlation grow with \(\Omega/\omega\)^4,12. Such non-trivial quantum vacuum bears resemblance with the dynamical Casimir effect and they are currently experimental efforts directed to the observation of this quantum vacuum radiation using non-adiabatic cavity quantum electrodynamics.

In our lab, we pioneered a new platform for ultrastrong coupling in the THz and mm-wave spectral regions based on inter-Landau level transitions in semiconductor heterostructures coupled to metallic and superconducting metasurfaces¹³. You can find more details about our research on this topic in this Section of our website.