Frequency Combs
This section is designed to give an overview of optical Frequency Combs, as well as current topics in their research and applications. It links to resources beyond the scope of the original research of the Faist group.
What is the experimental evidence that the QCL is an optical frequency comb?
What are the practical uses and consequences that the QCL is an optical frequency comb?
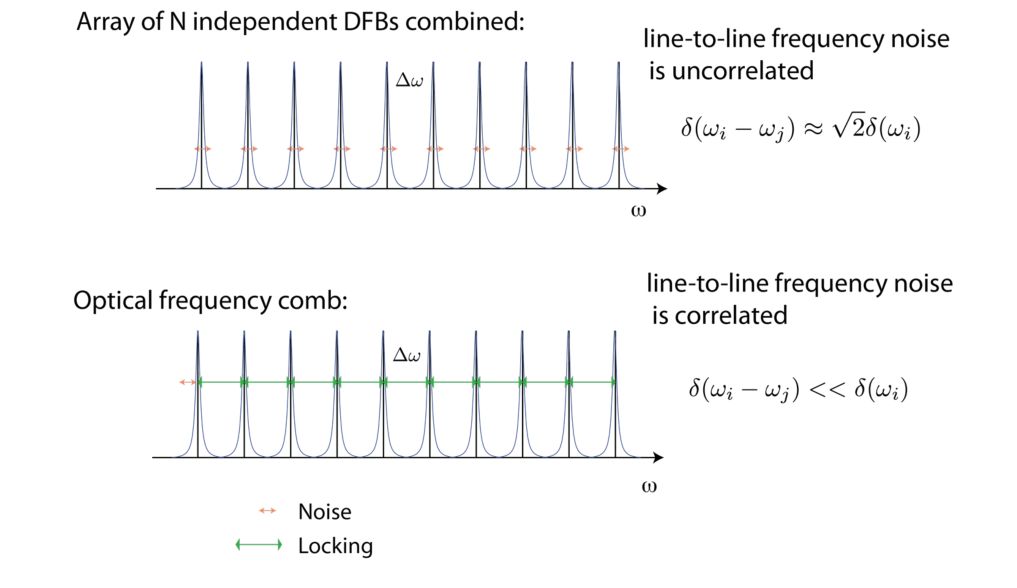
What is a comb?
A optical frequency comb is an optical source with equidistant optical modes [1], where the frequencies can be expressed using the equation:
$$ f_n=f_{CEO}+n\times f_r$$
In particular, what matters is that this equation holds even in the presence of noise. In other words, the noise can be fully expressed as a noise of \( f_{CEO}\) and \( f_r \) and, which as discussed at the end of this document, is a fact that has a very important consequences for spectroscopy. Such a property would not hold for an array of N independent optical sources finely tuned to be equidistant.
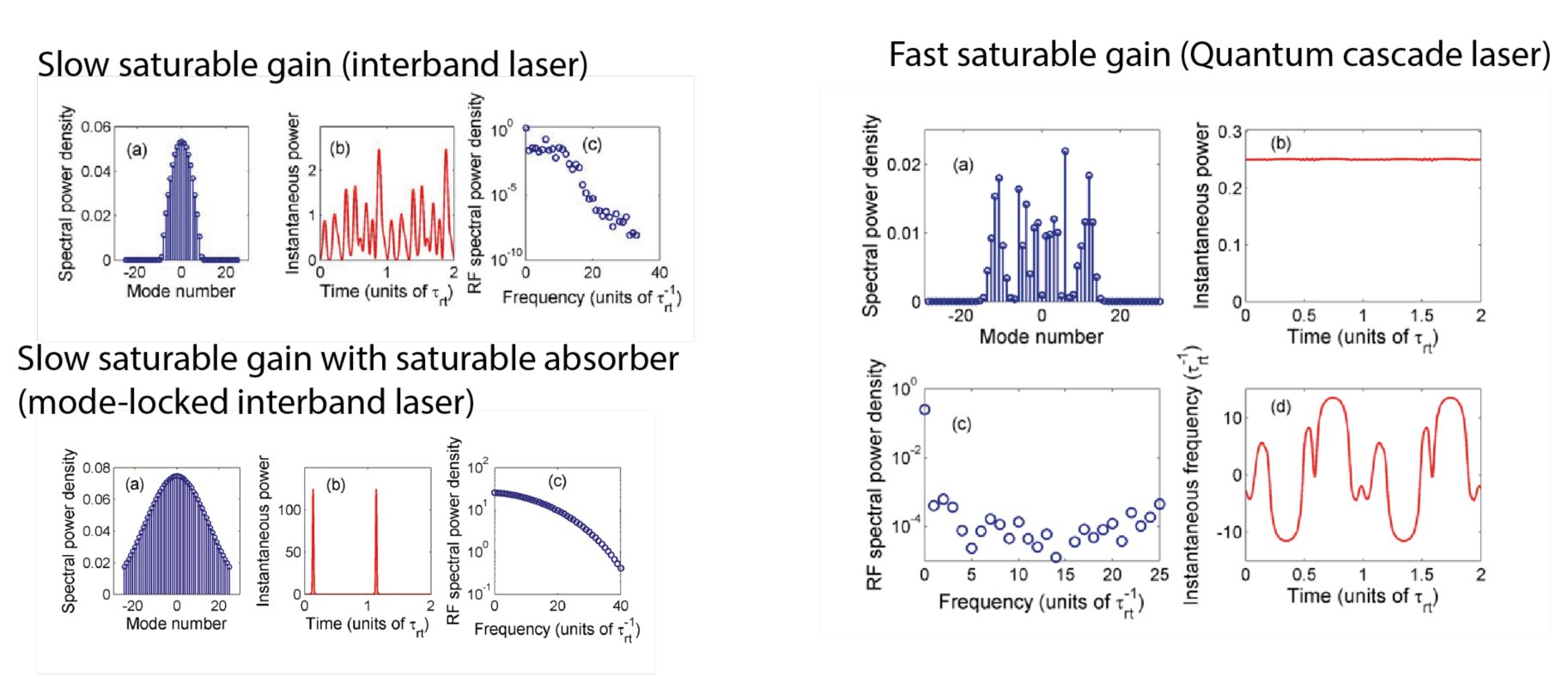
While this correlation between modes is usually achieved in mode-locked lasers with the use of a saturable absorber, it is obtained in quantum cascade lasers by the ultrafast non-linearity presented by the active region itself. Indeed, because of the very short upper state lifetime, the population inversion “follows” the intensity modulation created by the beating between the modes. This creats side bands via a four wave mixing process that has a Terahertz bandwidth [7]. These sidebands, in turn, can be seen as injection locking the Fabry-Perot modes of the free running laser. This process, running between all pairs of modes lock them together into a single coherent comb if the dispersion of the cavity is low enough.
What are the data showing that the QCL is an optical frequency comb?
Beatnote linewidth and beatnote spectroscopy [2]
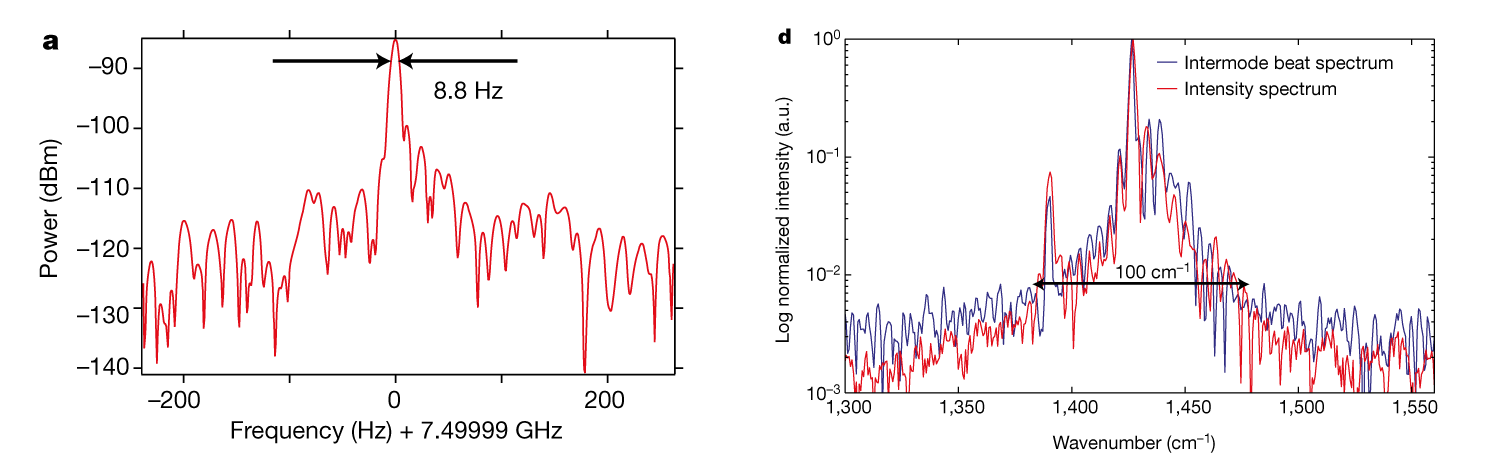
In our first external page Nature 2012 we showed that beating all the modes together created a beat-tone at the round trip frequency with a very narrow linewidth, as narrow as 8.8 Hz FWHM. Translated into a jitter, this linewidth corresponds to a 460 fs jitter in the frequency range of 20 kHz to 100 MHz. Essential to prove the comb operation was to additionally show that the beatnote was originating from the whole spectrum when and only when the laser was in the comb regime.
Equidistance from dual comb experiment [3]
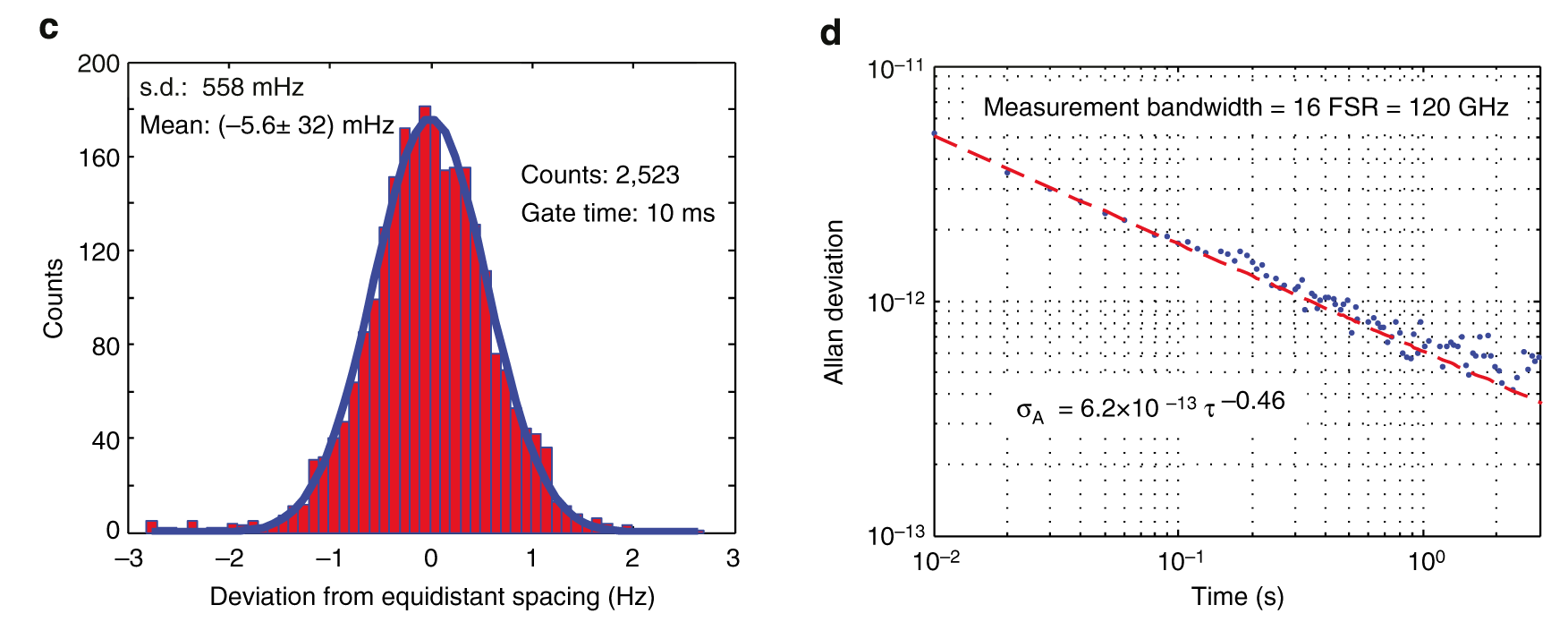
The next key experiment was the measurement of the equidistance of the comb lines to a relative value of 6x10-13 after averaging a few seconds. This measurement was obtained by comparing two QCL combs and beating them one against another. What was found was that in the 120 GHz optical bandwidth studied, the spacing of the modes was even to a 5 mHz accuracy. Strictly, it meant that the two combs had difference in GVD of 3 as2/mm. To achieve this result without the correlation of the modes brought by the four wave mixing would have required the two ridges of the QCL devices to have the exact same width to 4 femtometers! Recently, a similar experiment was performed in the group of Prof. de Natale (Ino-LENS, Florence) where a QCL comb was compared to a metrological comb based on an ultrafast laser, further confirming the comb nature of the QCL emission and enabling a measurement of the QCL comb phases.
Equidistance between non-comb sources:
What was measured to be \( \delta = 6\times 10^{-13} \) was the relative change in mode spacing across 120 GHz, the bandwidth represented by the three modes selected. For a typical residual GVD of the waveguide of 1000 fs/mm, the change of GVD between the two sources is \( \delta GVD = \delta^\ast GVD = 3\) as2mm-1 . Numerical simulations show that a change of device ridge width of that device by 1 µm modifies the GVD by 670 fs/mm. As a result the 3 as/mm difference would correspond to difference in ridge width of 4x10-9 µm!
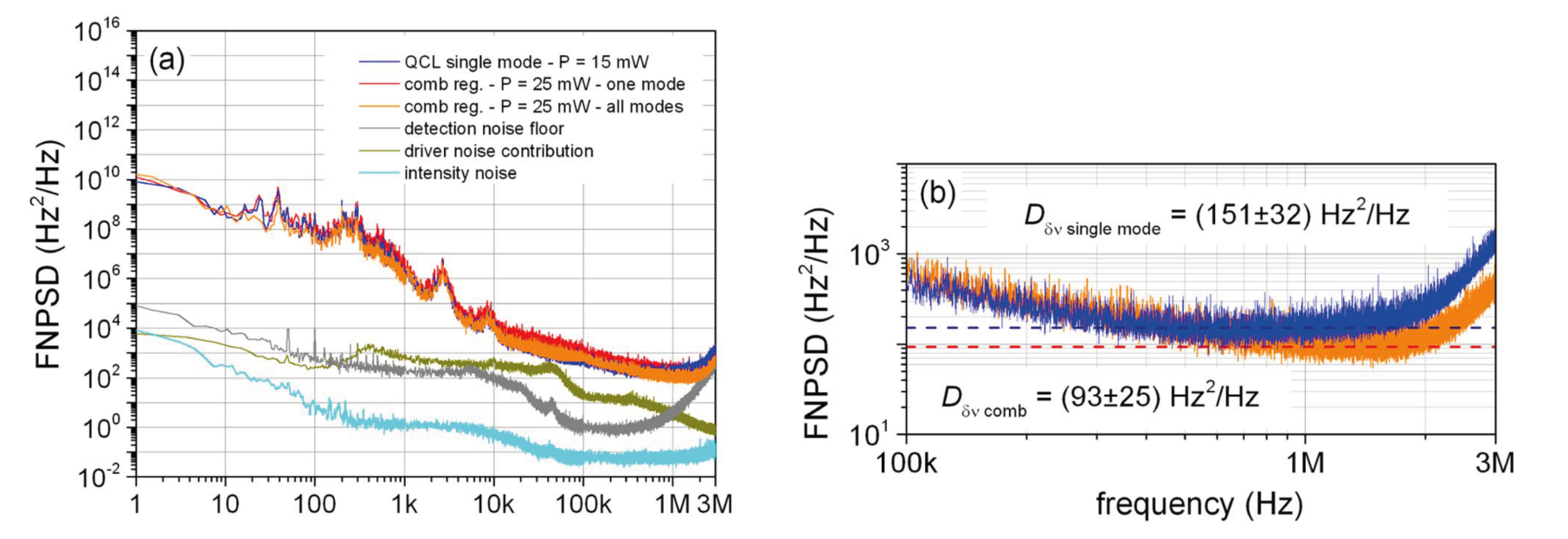
Optical linewidth of the comb [8]
One of the defining feature of a laser is its coherence, which is fundamentally limited by the so-called Schawlow-Townes limit to the linewidth. The latter expresses the linewidth as the ratio of the spontaneous emission rate to the total number of photon in the cavity and is therefore inversely proportional to the number of photons in the cavity. As a result, the fundamental limit for the linewidth of comb of 250 lines is 250 times narrower than for 250 individual laser sources equally spaced. We showed experimentally, using a high-finesse Fabry-Perot cavity as an optical discriminator, that a QCL comb exhibits a linewidth limited by the Schawlow-Townes relation and by its total output power and therefore that each line has a linewidth of the order of 270 Hz, equal to the ones measured in c.w. devices. This result is a very strong proof of comb operation and showed that the correlations induced by the four wave mixing extended to the quantum regime.
Measurements of the phases [4]
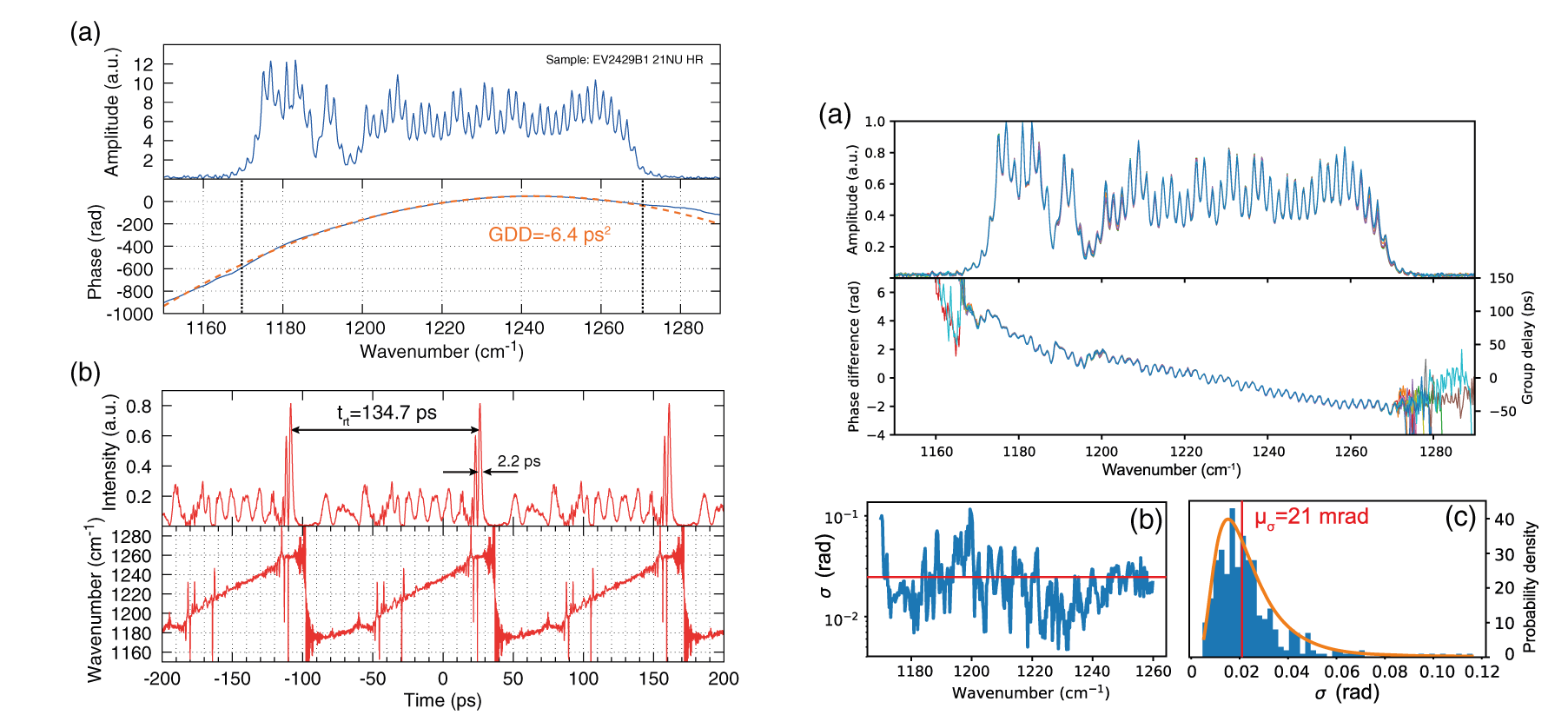
While all the measurements performed on mid-infrared QCL did show unambiguous proof of comb behavior and of the long-term stability of the phases of the optical modes, none of the measurements could retrieve the phases. A coherent beat-note spectroscopy measurement, in which the two quadratures of the beatnote are measured as a function of time delay in an interferometer is, however able to retrieve the phase difference between adjacent modes. The global phase is then retrieved after summing the phases differences.
This measurement (SWIFTS) was first performed in the THz by D. Burghoff in the group of Q. Hu [9] at MIT and repeated recently in our group using a mid-infrared quantum cascade laser [4]. Of course, such a measurement can only be successful If the phases are stable over a long period of time (at least during one scan of the interferometer). Actually, it was shown that not only are the phases stable and repeatable after temperature and current cycling, they follow close to a pure quadratic dependence in frequency. The result is a striking linear dependence of the instantaneous frequency as a function of time during one period of comb.
Compression of the pulses
The last result, is the compression of the output of the QCL comb into optical pulses using a standard dual grating, 4f compressor. The compression is enabled by the essentially quadratic nature of the global phase and the resulting linear chirp of the optical frequency with time. The resulting pulse length is 17 ps FWHM, limited by the residual deviation from pure parabolic behavior of the phase for both the laser and the compressor. Analysis of the pulse jitter can then be carried over, yielding a FWHM jitter of 0.6 \( \pm \) 0.2 ps in a frequency range of 20 kHz to 100 MHz.
Does it practically matter that the QCL is an optical frequency comb?
Coherent averaging of spectra
The fact that the QCL operates as a comb is not a result that would only raise pure academic interest; on the contrary it is very important because it enables low-noise multiheterodyne or dual comb spectroscopy. In this technique, the heterodyne beatnote between pairs of individual lines of a pair of optical frequency comb is measured by a fast detector. In this process, the frequency noise of the comb lines is transferred into the electrical signal. This noise, however, has a very special and highly correlated nature because it arises entirely from the noise of the offset frequency and the noise of the repetition rate of both combs. Because of this correlation, algorithms that take into account this correlation have enabled very low-noise measurements and extraction of the dual-comb signal from what originally would look like useless data. Our initial demonstration of dual-comb spectroscopy already partially implemented such approach [3], and recent published work [10-11] demonstrated the power of this technique. In many ways, the success of these de-noising techniques are real proofs of the comb nature of the QCL operation.
Is the behavior of QCL combs predicted theoretically?
Maxwell-Bloch model
The lack of pulses in the QCL comb emission made the usual solution of the Maxwell-Bloch formalism in the time domain difficult to interpret, because the telltale features of the comb operation appeared only in the frequency domain. A significant step was the introduction, by J. Khurgin, of a Maxwell-Bloch approach in which the emission is modelled by a set of coupled-mode equations in the frequency domain [6]. Interestingly, this approach had been already used by W.E. Lamb to explain the coupling of the three-mode laser [12]. The very nice feature of this approach is the fact that it treated self-phase and cross-phase modulation as well as spatial hole burning in a consistent approach. Numerical solutions of these equations showed the qualitative difference between the conventional mode-locking due to a saturable absorber and the comb operation through four wave mixing. This model was then further expanded to include material and waveguide dispersion as well as external modulation.
References:
[1] Udem, T.; Holzwarth, R.; Hansch, T., Optical frequency metrology. Nature 2002, 416 (6877), 233-237.
[2] Hugi, A.; Villares, G.; Blaser, S.; Liu, H. C.; Faist, J., Mid-infrared frequency comb based on a quantum cascade laser. Nature 2012, 492 (7428), 229-233.
[3] Villares, G.; Hugi, A.; Blaser, S.; Faist, J., Dual-comb spectroscopy based on quantum-cascade-laser frequency combs. Nature Communications 2014, 5, 1-9.
[4] Singleton, M.; Jouy, P.; Beck, M.; Faist, J., Evidence of linear chirp in mid-infrared quantum cascade lasers. Optica 2018, 5 (8), 948-953.
[5] Cappelli, F.; Villares, G.; Riedi, S.; Faist, J., Intrinsic linewidth of quantum cascade laser frequency combs. Optica 2015, 2 (10), 836-5.
[6] Khurgin, J. B.; Dikmelik, Y.; Hugi, A.; Faist, J., Coherent frequency combs produced by self frequency modulation in quantum cascade lasers. Applied Physics Letters 2014, 104 (8), 081118.
[7] Friedli, P.; Sigg, H.; Hinkov, B.; Hugi, A.; Riedi, S.; Beck, M.; Faist, J. r., Four-wave mixing in a quantum cascade laser amplifier. 2013, 102 (22), 222104.
[8] Cappelli, F.; Villares, G.; Riedi, S.; Faist, J., Intrinsic linewidth of quantum cascade laser frequency combs. In Optica, Optical Society of America: 2015; Vol. 2, pp 836-5.
[9] Burghoff, D.; Kao, T.-Y.; Han, N.; Chan, C. W. I.; Cai, X.; Yang, Y.; Hayton, D. J.; Gao, J.-R.; Reno, J. L.; Hu, Q., Terahertz laser frequency combs. Nature Photonics 2014, 8 (6), 462-467.
[10] Burghoff, D.; Yang, Y.; Hu, Q., Computational multiheterodyne spectroscopy. Science Advances 2016, 2 (11), -e1601227.
[11] Sterczewski, L. A.; Westberg, J.; Wysocki, G., Computational coherent averaging for free-running dual-comb spectroscopy. arXiv.org 2018, physics.ins-det.
[12] Lamb, J., W E, Theory of an optical maser. Physical Review 1964, 134 (6A), A1429-A1450.